可以解釋一下嗎?符號搞得不懂?
2020-08-12 11:34 pm
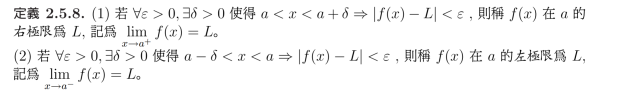
回答 (1)
2020-08-13 6:37 am
一般極限是指 "雙邊極限", 或說 "無限制方向的極限",
也就是: 不管 x 是如何向 a 逼近的, f(x) 都趨近 L.
而這裡是定義 "單邊極限", 也就是 x 只從 a 的左邊,
或只從 a 的右邊逼近 a.
以左極限來說, 就是:
只要 x 在 a 的左邊, 並且夠接近 a (但 x≠a),
則 f(x) 就很接近 L.
精確地講, 就是:
對任意 ε > 0,
都能找到 δ > 0, 使得
只要 a-δ < x < a, 就得到 |f(x)-L| < ε.
注意條件 "a-δ < x < a" 就是
x < a 並且 0 < |x-a| < δ.
類似地, x→a+ 時 f(x)→L 就是說:
對任意 ε > 0,
都能找到 δ > 0, 使得
只要 a+δ > x > a, 就得到 |f(x)-L| < ε.
白話說就是:
只要 x 在 a 的右邊, 並且夠接近 a (但 x≠a),
則 f(x) 就很接近 L.
也就是: 不管 x 是如何向 a 逼近的, f(x) 都趨近 L.
而這裡是定義 "單邊極限", 也就是 x 只從 a 的左邊,
或只從 a 的右邊逼近 a.
以左極限來說, 就是:
只要 x 在 a 的左邊, 並且夠接近 a (但 x≠a),
則 f(x) 就很接近 L.
精確地講, 就是:
對任意 ε > 0,
都能找到 δ > 0, 使得
只要 a-δ < x < a, 就得到 |f(x)-L| < ε.
注意條件 "a-δ < x < a" 就是
x < a 並且 0 < |x-a| < δ.
類似地, x→a+ 時 f(x)→L 就是說:
對任意 ε > 0,
都能找到 δ > 0, 使得
只要 a+δ > x > a, 就得到 |f(x)-L| < ε.
白話說就是:
只要 x 在 a 的右邊, 並且夠接近 a (但 x≠a),
則 f(x) 就很接近 L.
收錄日期: 2021-05-04 02:36:31
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200812153457AALdKVS

