A certain reaction has the form
aA → Products
At a particular temperature, concentration versus time data were collected.
A plot of 1/[A] vs t (in seconds) gave a straight line with a slope of 6.90 × 10-2.
If the original concentration (at t = 0) is 0.100 M, calculate the second half-life (in seconds) for this experiment.
Note: Because of online schooling, we're using this online learning program and well, this is the only problem I need to finish. I have input the 145 min (which was stupid), then I input 8696s (which was wrong). I know how to set up the problem, for second half-lifes we use the equation:
t1/2 = 1/k[A]0
which would be:
t1/2= 1/(0.0690)(0.100)
t1/2= 144.9 = 145 min
145 min = 8695.6s = 8696s
for this problem, right?
I don't know why it keeps telling me I'm wrong, any help is appreciated. Please correct me if I'm wrong. Help!
Chemistry Help - Kinetics (Half-life)?
2020-08-12 12:58 pm
回答 (3)
2020-08-12 2:29 pm
The integrated form of second-order reaction:
1/[A] = kt + (1/[A]ₒ)
where [A] and t are variables, while k and [A]ₒ are constant.
If the plot of 1/[A] vs t gives a straight line, the reaction is second-order. The slope is equal to k, and thus
k = 6.92 × 10⁻² M⁻¹ s⁻¹
For this second-order reaction, 1/[A] = kt + (1/[A]ₒ)
When [A] = [A]ₒ/2, t = t½:
2/[A]ₒ = kt½ + (1/[A]ₒ)
Then, half-life, t½
= 1/(k[A]ₒ)
= 1/[(6.90 × 10⁻²) × 0.100] s
= 145 s
====
Your calculation is correct, but the unit of time should be seconds instead of minutes.
1/[A] = kt + (1/[A]ₒ)
where [A] and t are variables, while k and [A]ₒ are constant.
If the plot of 1/[A] vs t gives a straight line, the reaction is second-order. The slope is equal to k, and thus
k = 6.92 × 10⁻² M⁻¹ s⁻¹
For this second-order reaction, 1/[A] = kt + (1/[A]ₒ)
When [A] = [A]ₒ/2, t = t½:
2/[A]ₒ = kt½ + (1/[A]ₒ)
Then, half-life, t½
= 1/(k[A]ₒ)
= 1/[(6.90 × 10⁻²) × 0.100] s
= 145 s
====
Your calculation is correct, but the unit of time should be seconds instead of minutes.
2020-08-12 10:17 pm
micatkie's answer is very nicely worked through and correctly calculates the first half-life to be 145 seconds.
However, the question says "calculate the second half-life".
Because this is a second order reaction, the half-life is not constant, and depends on the initial concentration. So, the second half-life for this reaction will begin with [A]o = 0.050 M.
So, the second half-life is:
t1/2 = 1/k[A]
t1/2 = 1/(6.92X10^-2 M^-1s^-1) (0.050 M) = 289 seconds
However, the question says "calculate the second half-life".
Because this is a second order reaction, the half-life is not constant, and depends on the initial concentration. So, the second half-life for this reaction will begin with [A]o = 0.050 M.
So, the second half-life is:
t1/2 = 1/k[A]
t1/2 = 1/(6.92X10^-2 M^-1s^-1) (0.050 M) = 289 seconds
2020-08-12 1:03 pm
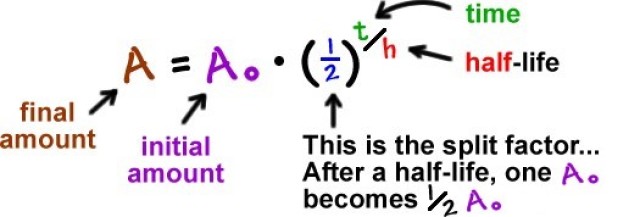
True half-life is in the format
A = A₀ (1/2)^(t/h)
A = A₀ (1/2)^(t/h)
收錄日期: 2021-04-24 07:57:22
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200812045829AA42DKH

