更新1:
更新:這是小六升中一的題目,請不要用太深奧的數式回答🙏🏻
更新:這是小六升中一的題目,請不要用太深奧的數式回答🙏🏻
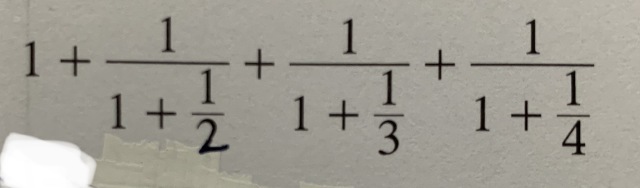
收錄日期: 2021-04-24 07:54:32
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200803103836AAxYb4s