Maths problem:how to do (c), i found out angle AOB=68° and radius is 4.82 cm. Thanks?
2020-07-23 4:37 pm
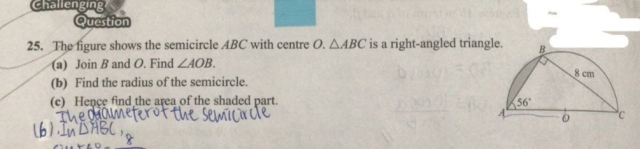
回答 (1)
2020-07-23 8:19 pm
✔ 最佳答案
(a) From △AOB :∵ radius of semicircle, r = OA = OB,
∴ △AOB is an isos.△
=> ∠ABO = 56⁰ (base ∠s, isos.△)
So, ∠AOB = 180⁰-2(56⁰) = 68⁰
(b) From △ABC : ∠C=90-56=34⁰
From △BOC :
r² = 8²+r²-2(8r) cos 34⁰
0 = 64-16r cos 34⁰
r cos 34⁰ = 4
∴ r = 4/cos 34⁰ = 4.82 cm (to 2 dec.pl.)
# (a),(b) 都答對 !! *\(^o^)/*
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(c) area of △AOB=½ r*r sin 68⁰=½(4.82)²sin68⁰
area of sector AOB=πr²(68⁰/360⁰)=π(4.82)²(68⁰/360⁰)
∴ area of shaded part
= π(4.82)²(68⁰/360⁰) - ½(4.82)²sin68⁰
= (4.82)² [(68⁰/360⁰)π - (sin68⁰)/2]
= 3.02 (to 2 dec.pl.)
收錄日期: 2021-04-24 07:56:45
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200723083745AAbea7A

