Trig help ?

Method 1:

a/sin(A) = c/sin(C)  (sine law)
24.2/sin(A) = 18.3/sin(44.6°)
sin(A) = sin(44.6°) × (24.2/18.3)
sin(A) = 0.9285
A = 68.2°, (180 - 68.2)°
A = 68.2°, 111.8°

Two triangles can be drawn because the sum of interior angles does not exceed 180° for each value of A.

The answer: 2

====
Method 2:

c² = a² + b² - 2 a b cosC   (cosine law)
18.3² = 24.2² + b² - 2 × 24.2 × b × cos(44.6°)
b² - 34.462b + 250.75 = 0
b = [34.462 ± √(34.462² - 4×250.75)]/2
b = 10.4, 24.0

Two triangles can be drawn because there are two positive values for b.

The answer: 2

Use the Cosine Rule:
c^2 = a^2 + b^2 - 2ab*cos(C)
18.3^2 = 24.2^2 + b^2 - 2*24.2*b*cos(44.6°)
334.89 = 585.64 + b^2 - 48.4b*cos(44.6°)
b^2 - 48.4b*cos(44.6°) + 585.64 - 334.89 = 0
b^2 - 48.4*cos(44.6°) *b + 250.75 = 0
Use the Quadratic Formula:
b = (-(-48.4*cos(44.6°) ) +/- sqrt((-48.4*cos(44.6°) )^2 - 4*1*250.75)) / (2*1)
b = (48.4*cos(44.6°) +/- sqrt(2342.56*cos^2(44.6°) - 1003)) / 2
b =~ 10.437 or 24.025

The answer is 2.

There are several ways to start in on this. I strongly recommend that you develop a sense for the geometry of the figure. Until you have perfected that skill, get into a habit of sketching the figure at something close to a consistent scale. Begin this one with the sine rule.

sin(A)/a = sin(C)/c
sin(A) = asin(C)/c
sin(A) = 24.2sin(44.6°)/18.3
sin(A) ≈ 0.93
sin(A) < 1

With sin(A) being less than 1, there must be at least one solution. Since a is greater than c, ∠A can be obtuse, which means there must be two solutions, and that is the answer to your question.

Were sin(A) equal to 1, there would be only the right angle solution for ∠A, and there would be exactly one triangle satisfying all conditions.

Were sin(A) greater than 1, there would be zero solutions, because the sine function cannot reach above the value 1.

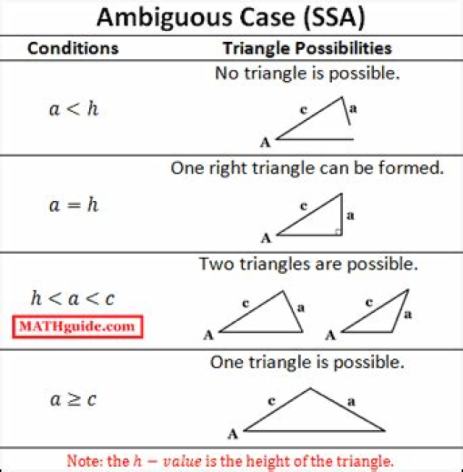
What I have shown here addresses this problem, but does not address all problems in which limited information is given for a triangle. That image attached to Friendly's answer looks quite useful. It might be worth saving.

Sketch the "triangle" with the given values.

Since we have side, side, angle (SSA), this is an ambiguous case

I, myself, have no clue how to solve this, but trust in this random image I found off the internet