{(3/4)^1.5} *{(2/3)^1.5} math question?
回答 (6)
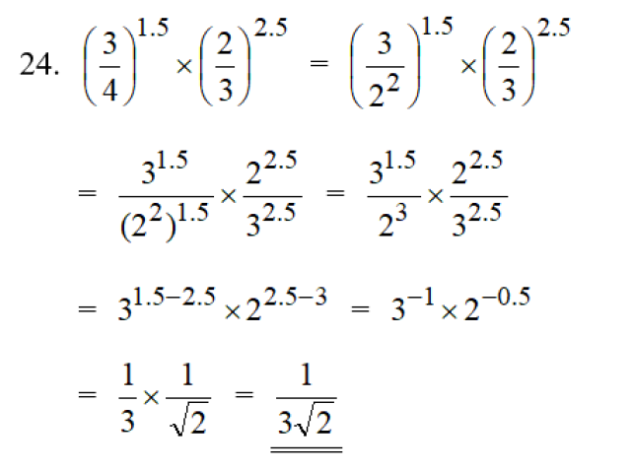
2020-07-21 12:06 am
a^(b * c) = (a^b)^c or (a^c)^b. Either one is valid
3/2 = 3 * (1/2)
5/2 = 5 * (1/2)
(a * b)^c = (a^c) * (b^c)
(3/4)^(3/2) * (2/3)^(5/2) =>
((3/4)^3)^(1/2) * ((2/3)^5)^(1/2) =>
((3/4)^3 * (2/3)^5)^(1/2) =>
(3^3 * 2^5 / (4^3 * 3^5))^(1/2) =>
(3^(3 - 5) * 2^5 / (2^2)^3)^(1/2) =>
(3^(-2) * 2^5 / 2^6)^(1/2) =>
(3^(-2) * 2^(5 - 6))^(1/2) =>
(3^(-2) * 2^(-1))^(1/2) =>
3^(-2 * (1/2)) * 2^(-1 * (1/2)) =>
3^(-1) * 2^(-1/2) =>
(1/3) * (1/sqrt(2)) =>
1/(3 * sqrt(2))
3/2 = 3 * (1/2)
5/2 = 5 * (1/2)
(a * b)^c = (a^c) * (b^c)
(3/4)^(3/2) * (2/3)^(5/2) =>
((3/4)^3)^(1/2) * ((2/3)^5)^(1/2) =>
((3/4)^3 * (2/3)^5)^(1/2) =>
(3^3 * 2^5 / (4^3 * 3^5))^(1/2) =>
(3^(3 - 5) * 2^5 / (2^2)^3)^(1/2) =>
(3^(-2) * 2^5 / 2^6)^(1/2) =>
(3^(-2) * 2^(5 - 6))^(1/2) =>
(3^(-2) * 2^(-1))^(1/2) =>
3^(-2 * (1/2)) * 2^(-1 * (1/2)) =>
3^(-1) * 2^(-1/2) =>
(1/3) * (1/sqrt(2)) =>
1/(3 * sqrt(2))
2020-07-21 1:16 am
Put E = ((3/4)^(1.5)*((2/3)^(2.5)) = (3^(1.5-2.5))(2^(2.5-3) = (1/3)(1/rt2) = 1/(3rt2).
Option C. gives correct answer.
Option C. gives correct answer.
2020-07-21 12:27 am
{(3/4)^1.5} * {(2/3)^2.5} = 0.235702
2020-07-21 12:11 am
[(3/4)^(1.5)]•[(2/3)^(2.5)]
= [3^(1.5)/3^(2.5)]•[2^(2.5)/4^(1.5)]
= [3^(1.5-2.5)]•[2^(2.5)/2^(2•1.5)]
= 3^(-1)•2^(-0.5)
= (1/3)(1/√2)
= 1/(3√2)
= [3^(1.5)/3^(2.5)]•[2^(2.5)/4^(1.5)]
= [3^(1.5-2.5)]•[2^(2.5)/2^(2•1.5)]
= 3^(-1)•2^(-0.5)
= (1/3)(1/√2)
= 1/(3√2)
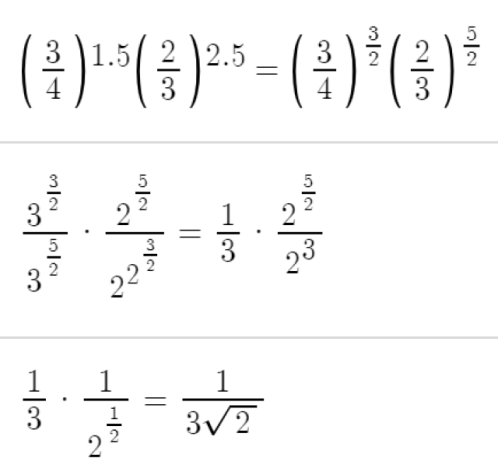
收錄日期: 2021-04-24 07:57:13
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200720160211AAqmivr