關於保守向量場的必要條件之推導?
2020-07-19 9:55 pm
關於保守場的必要條件:若向量F(x,y)=<F1(x,y),F2(x,y)>是xy平面區域D上的保守場,F1及F2在D上有連續的一階偏導函數,則在D上∂F1/∂y = ∂F2/∂x請問如何證明,光用看得有點不是很懂
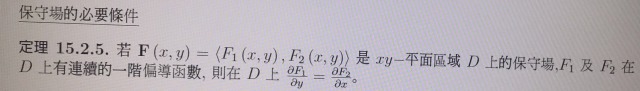
回答 (1)
2020-07-20 7:28 am
✔ 最佳答案
F 是一個保守向量場的定義是:存在一純量場 φ, 使 F = ▽φ.
也就是說:
如果一個向量場是某純量函數的梯度, 就稱它是保守的.
而對一個多實變量實數值函數, 可證明若其所有二階偏
導數(在某點)運績, 則其偏微順序(在該點)是可互換的.
也就是說: 先對 x 做偏微再對 y 做偏微, 和先對 y 做偏
微再對 x 做偏微, 其結果相同.
換個方式來說:
若 f(x,y,...) 在 (a,b,...) 的所有二階偏導數都是連續的,則
{f(a+h,b+k,...)-f(a+h,b,...)-f(a,b+k,...)+f(a,b,...)}/(hk)
先令 h→0 再令 k→0 而求取的極限值, 與先令 k→0 再
令 h→0 求取的極限值一致.
證明:
設 A = D_{yx}f(a,b) 表示 f(x,y) 在 (a,b) 先對 y 再對 x
偏微的結果.
由於連續性, 對任意 ε > 0, 只要 (x,y) 夠靠近 (a,b) 即保
證 |D_{yx}f(x,y) - A| < ε.
令
Δf(a,b) = f(a+h,b+k)-f(a+h,b)-f(a,b+k)+f(a,b)
則應用單變量函數的均值定理, 存在 s 介於 a 與 a+h 之
間, t 介於 b 和 b+k 之間, 使得 Δf(a,b) = hk D_{yx}f(s,t).
這是因
Δf(a,b) = (f(a+h,b+k)-f(a,b+k)) - (f(a+h,b)-f(a,b))
= h (D_xf(s,b+k) - D_xf(s,b))
= h (k D_y D_x f(s,t))
= hk D_{yx}f(s,t)
所以, 只要 (a+h,b+k) 足夠靠近 (a,b), 也就是說 h, k 夠
小, 則 |Δf(a,b)/(hk) - A| < ε.
固定 k, 令 h→0, 則因一階偏導數在 (a,b) 鄰近都存在在
(因二階偏導數的存在), 故前式蘊涵
|(D_x(a,b+k)-D_x(a,b))/k - A| ≦ ε
由於 ε 是任意正數, 且上式對所有足夠小的 k≠0 都成立,
因此得 D_{xy}f(a,b) 存在且等於 A = D_{yx}f(a,b).
以上其實證明了一個微分順序的二階偏導數存在且連績,
則 另一個順序的二階偏導數也存在, 且二者相等. 那麼,
如果已知兩個順序的二階偏導數都存在且連續, 則二者
當然相等.
對一個保守向量場 F 來說,
∫_{(a,b)→(c,d)} F_1 dx + F_2 dy
= ∫_{(a,b)→(c,b)} F_1 dx + F_2 dy
+ ∫{(c,b)→(c,d)} F_1 dx + F_2 dy
= ∫_{(a,b)→(c,b)} F_1 dx + ∫{(c,b)→(c,d)} F_2 dy
= φ(c,b) - φ(a,b) + φ(c,d) - φ(c,b)
= φ(c,d) - φ(a,b)
= ∫_{(a,b)→(a,d)} F_1 dx + F_2 dy
+ ∫{(a,d)→(c,d)} F_1 dx + F_2 dy
事實上如果 F 是一個保守向量場, 則 F 沿任何由 (a,b)
到 (c,d) 的連續曲線 C 積分結果是一樣的, 上面先水平
(a,b)→(c,b) 再垂直 (c,b)→(c,d) 及先垂直 (a,b)→(a,d)
再水平 (a,d)→(c,d) 只是兩種特殊路徑而已. 這種現象
稱為路徑無關 (path independence). 由於路徑無關,
所以如果積分路是一個閉環, (c,d) = (a,b), 則積分結
果為 0.
收錄日期: 2021-05-04 02:25:27
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200719135514AA7Lq9d

