write each expression as a single logarithm in simplest form. logA/2 - logB/3?
回答 (5)
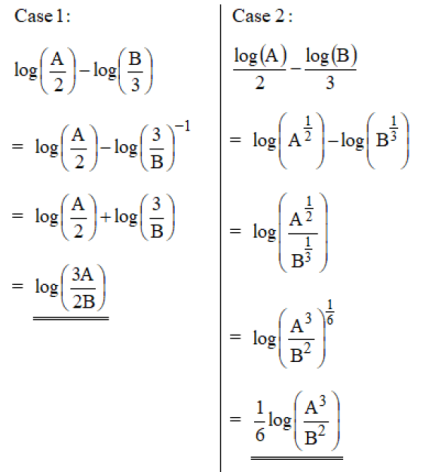
2020-07-19 10:52 am
depends...if this is log ( A / 2) - log (B/.3) then log( 3A/(2B)).....if log A / 2 - log B / 3 then log ( √ A / ³√B )....(...) are useful in math
2020-07-19 1:54 pm
If that is:
log(a / 2) - log(b / 3)
Then the difference of two logs of the same base is the same as the quotient of the two logs:
log[(a / 2) / (b / 3)]
Division is the same as the multiplication of the reciprocal, so:
log[(a / 2) * (3 / b)]
log[3a / (2b)]
log(a / 2) - log(b / 3)
Then the difference of two logs of the same base is the same as the quotient of the two logs:
log[(a / 2) / (b / 3)]
Division is the same as the multiplication of the reciprocal, so:
log[(a / 2) * (3 / b)]
log[3a / (2b)]
2020-07-19 12:18 pm
log(A/2) - log(B/3) = log((A/2)/(B/3)) = log(3A/2B).
2020-07-19 12:08 pm
logA/2 - logB/3 =
.......A/2
log ------ =
.......B/3
.......3A
log ----- ...............ANS
.......2B
.......A/2
log ------ =
.......B/3
.......3A
log ----- ...............ANS
.......2B
收錄日期: 2021-04-18 18:32:55
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200719024342AALsAM8