find and simplify the second derivative using derivative properties (revision help)?
2020-06-10 12:24 pm
Hi! I'm just needing a little help on fixing the errors I made on a worksheet regarding finding and simplifying the second derivative. For part (a), I was told that for the last chain rule - the derivative of 4x^2 is 8x, so I believe that this feedback is just telling me that my final answer should be f"(x) = 2x(1-8x)^-3/2, but then when I worked out the problem again, I was getting the answer (8x)/((1-4x^2)^ 3/2), so now I am struggling to figure out which is correct, so if someone could show me how to properly work through this problem, I would majorly appreciate it.
回答 (3)
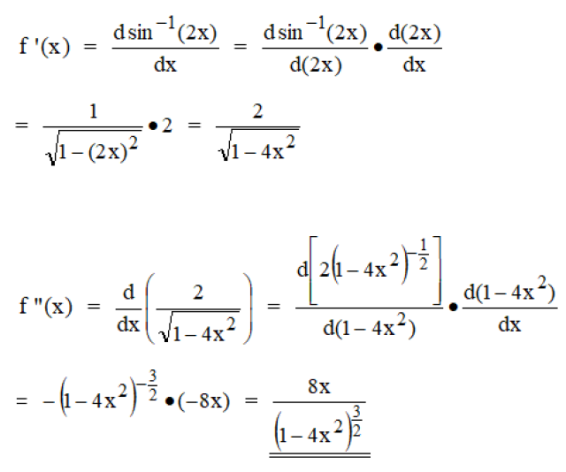
2020-06-10 8:00 pm
From your solution 2nd derivative part.
You forgot to differentiate 1 - 4x^2 from (1 - 4x^2)^(-3/2)
f''(x) = 2(-1/2)(1 - 4x^2)^(-3/2) d/dx - 8x..
f''(x) = 8x (1 - 4x^2)^(-3/2)
..................8x
f''(x) =----------------------.. Answer//
.........(1 - 4x^2)^(3/2)
You forgot to differentiate 1 - 4x^2 from (1 - 4x^2)^(-3/2)
f''(x) = 2(-1/2)(1 - 4x^2)^(-3/2) d/dx - 8x..
f''(x) = 8x (1 - 4x^2)^(-3/2)
..................8x
f''(x) =----------------------.. Answer//
.........(1 - 4x^2)^(3/2)
2020-06-10 6:29 pm
You state that f ''(x) = 2(d/dx)(1 - 4x²)⁻¹/²
Now, (d/dx)(1 - 4x²)⁻¹/² => (-8x)(-1/2)(1 - 4x²)⁻³/²
i.e. 4x(1 - 4x²)⁻³/²
Hence, 2(d/dx)(1 - 4x²)⁻¹/² => 2[4x(1 - 4x²)⁻³/²]
=> 8x(1 - 4x²)⁻³/²
or, 8x/(1 - 4x²)³/²
:)>
Now, (d/dx)(1 - 4x²)⁻¹/² => (-8x)(-1/2)(1 - 4x²)⁻³/²
i.e. 4x(1 - 4x²)⁻³/²
Hence, 2(d/dx)(1 - 4x²)⁻¹/² => 2[4x(1 - 4x²)⁻³/²]
=> 8x(1 - 4x²)⁻³/²
or, 8x/(1 - 4x²)³/²
:)>
收錄日期: 2021-04-18 18:32:00
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200610042411AAUAs5G