A curve has a general equation of the form Ax²+By²+F=0. If it passes through (4,0) and (0,3), find its specific equation.?
2020-06-07 7:51 pm
回答 (2)
2020-06-07 8:06 pm
Ax² + By² + F = 0 …… [1]
The curve passive through (4, 0).
Plug x = 4 and y = 0 into [1]:
A(4)² + B(0)² + F = 0
16A + F = 0
A = -F/16
The curve passive through (0, 3).
Plug x = 0 and y = 3 into [1]:
A(0)² + B(3)² + F = 0
9B + F = 0
B = -F/9
The equation is:
(-F/16)x² + (-F/9)y² + F = 0
[(-1/16)x² + (-1/9)y² + 1] * (-1) * 16 * 9 = 0
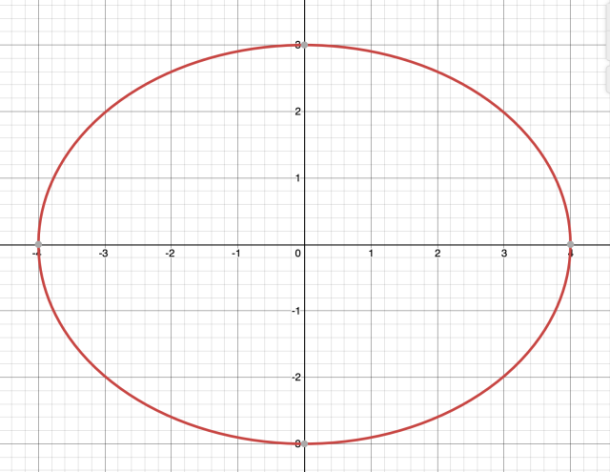
9x² + 16y² - 144 = 0
The curve passive through (4, 0).
Plug x = 4 and y = 0 into [1]:
A(4)² + B(0)² + F = 0
16A + F = 0
A = -F/16
The curve passive through (0, 3).
Plug x = 0 and y = 3 into [1]:
A(0)² + B(3)² + F = 0
9B + F = 0
B = -F/9
The equation is:
(-F/16)x² + (-F/9)y² + F = 0
[(-1/16)x² + (-1/9)y² + 1] * (-1) * 16 * 9 = 0
9x² + 16y² - 144 = 0
2020-06-07 8:19 pm
Ax²+By²+F=0
plug in the two points
A4²+B0²+F=0
A0²+B3²+F=0
16A + F = 0
9B + F = 0
2 eq in 3 unknowns, there is no one solution
–F = 16A = 9B
possible solutions:
A = 9, B = 16, F = –9•16
9x² + 16y² – 144 = 0
plug in the two points
A4²+B0²+F=0
A0²+B3²+F=0
16A + F = 0
9B + F = 0
2 eq in 3 unknowns, there is no one solution
–F = 16A = 9B
possible solutions:
A = 9, B = 16, F = –9•16
9x² + 16y² – 144 = 0
收錄日期: 2021-04-18 18:31:17
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200607115102AAvrohA
