How do I prove tan(theta/2)= sin(theta)/1+cos(theta) for theta in quadrant one?
2020-05-25 8:46 pm
What steps must I take to solve this problem. Please help! Thank you so much in advance!
回答 (2)
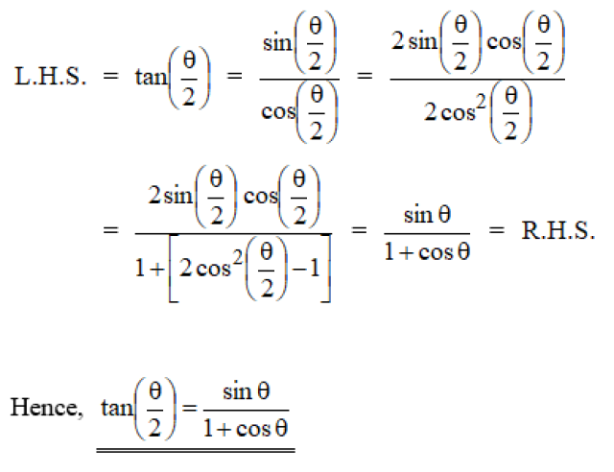
2020-05-25 9:20 pm
sin2θ = 2sinθcosθ and cos2θ = 2cos²θ - 1
so, sinθ = 2sin(θ/2)cos(θ/2) and cosθ = 2cos²(θ/2) - 1
Then, sinθ/(1 + cosθ) = [2sin(θ/2)cos(θ/2)]/[1 + 2cos²(θ/2) - 1]
Hence, sinθ/(1 + cosθ) = 2sin(θ/2)cos(θ/2)]/2cos²(θ/2)
i.e. 2sin(θ/2)/2cos(θ/2) => sin(θ/2)/cos(θ/2) = tan(θ/2)
:)>
so, sinθ = 2sin(θ/2)cos(θ/2) and cosθ = 2cos²(θ/2) - 1
Then, sinθ/(1 + cosθ) = [2sin(θ/2)cos(θ/2)]/[1 + 2cos²(θ/2) - 1]
Hence, sinθ/(1 + cosθ) = 2sin(θ/2)cos(θ/2)]/2cos²(θ/2)
i.e. 2sin(θ/2)/2cos(θ/2) => sin(θ/2)/cos(θ/2) = tan(θ/2)
:)>
收錄日期: 2021-05-01 01:03:27
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200525124620AAnU70F