Triangle word problem help?

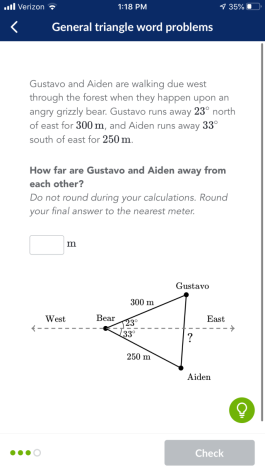
Point B: Bear
Point G: Gustavo
Point A: Aiden

GA² = BG² + BA² - 2 × BG × BA × cos(∠GBA)   (cosine law)
GA² = [300² + 250² - 2 × 300 × 250 × cos(23° + 33°)] m²
GA = √[300² + 250² - 2 × 300 × 250 × cos(56°)] m
GA = 262 m

The answer: 262 m

We can apply the 'cosine rule' to get:

?² = 300² + 250² - 2(300)(150)cos56°

so, ?² = 152500 - 90000cos56°

Then, ?² = 102172.6387

Hence, ? = √102172.6387 => 320 metres

Bonus question: ''How far would the bear have to run in order to eat Gustavo, followed by Aiden, then return home?''

:)>

 

sin(23) x 300 + sin(33) x 250
= 253.379097 m
I found this by finding the length  of straight line from Gustavo to the line in which the bear was
sin(23) = opposite/hypotenuse
sin(23) = opposite/300
opposite = sin(23) x 300
Then i found the length  of straight line from aiden to the line in which the bear was

sin(23) = opposite/hypotenuse 
sin(23) = opposite/250
opposite = sin(23) x 250

By adding them up you can calculate the total distance between Gustavo and aiden