(-3, -2) (-2, -3) (-4, -3) ?
2020-05-12 2:10 pm
Write the standard form of the equation of the circle that passes through the points with the given coordinates. Then identify the center and radius.
回答 (4)
2020-05-12 3:54 pm
Let (x - h)² + (y - k)² = r² be the equation of the circle.
Substitute x = -3 and y = -2 into the equation:
(-3 - h)² + (-2 - k)² = r²
(h + 3)² + (k + 2)² = r² …… [1]
Substitute x = -2 and y = -3 into the equation:
(-2 - h)² + (-3 - k)² = r²
(h + 2)² + (k + 3)² = r² …… [2]
Substitute x = -4 and y = -3 into the equation:
(-4 - h)² + (-3 - k)² = r²
(h + 4)² + (k + 3)² = r² …… [3]
[1] = [2]:
(h + 3)² + (k + 2)² = (h + 2)² + (k + 3)²
h² + 6h + 9 + k² + 4k + 4 = h² + 4h + 4 + k² + 6k + 9
2k = 2h
k = h …... [4]
[2] = [3]:
(h + 2)² + (k + 3)² = (h + 4)² + (k + 3)²
(h + 2)² = (h + 4)²
h² + 4h + 4 = h² + 8h + 16
4h = -12
h = -3
Substitute h = -3 into [4]:
k = -3
Substitute h = -3 and k = -3 into [1]:
(-3 + 3)² + (-1 + 2)² = r²
r² = 1
Hence, the equation of the circle is:
(x + 3)² + (y + 3)² = 1
Substitute x = -3 and y = -2 into the equation:
(-3 - h)² + (-2 - k)² = r²
(h + 3)² + (k + 2)² = r² …… [1]
Substitute x = -2 and y = -3 into the equation:
(-2 - h)² + (-3 - k)² = r²
(h + 2)² + (k + 3)² = r² …… [2]
Substitute x = -4 and y = -3 into the equation:
(-4 - h)² + (-3 - k)² = r²
(h + 4)² + (k + 3)² = r² …… [3]
[1] = [2]:
(h + 3)² + (k + 2)² = (h + 2)² + (k + 3)²
h² + 6h + 9 + k² + 4k + 4 = h² + 4h + 4 + k² + 6k + 9
2k = 2h
k = h …... [4]
[2] = [3]:
(h + 2)² + (k + 3)² = (h + 4)² + (k + 3)²
(h + 2)² = (h + 4)²
h² + 4h + 4 = h² + 8h + 16
4h = -12
h = -3
Substitute h = -3 into [4]:
k = -3
Substitute h = -3 and k = -3 into [1]:
(-3 + 3)² + (-1 + 2)² = r²
r² = 1
Hence, the equation of the circle is:
(x + 3)² + (y + 3)² = 1
2020-05-12 6:23 pm
Solving the midpoint of the circle using the coordinate (-2,-3),(-4,-3)
mid = [(- 2 - 4)/2, (- 3 - 3)/2]
mid = (-3,-3)
our center will be (-3,-3)
Solving for the radius from the standard equation of the circle from point (-3,-2)
(x - h)^2 + (y - k)^2 = r^2
[-3 - (-3)]^2 + [-2 - (-3)]^2 = r^2
1 = r^2
The equation of the circle is
(x + 3)^2 + (x + 3)^2 = 1.. Answer//
where the Center is C(-3,-3) and the radius is 1
mid = [(- 2 - 4)/2, (- 3 - 3)/2]
mid = (-3,-3)
our center will be (-3,-3)
Solving for the radius from the standard equation of the circle from point (-3,-2)
(x - h)^2 + (y - k)^2 = r^2
[-3 - (-3)]^2 + [-2 - (-3)]^2 = r^2
1 = r^2
The equation of the circle is
(x + 3)^2 + (x + 3)^2 = 1.. Answer//
where the Center is C(-3,-3) and the radius is 1
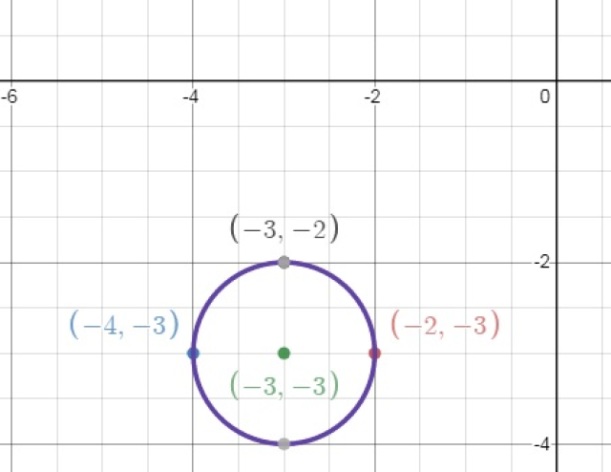
2020-05-12 5:15 pm
Let me label those points A(-3, -2), B(-2, -3), and C(-4, -3).
Using the slopes, it is clear that lines AB and AC are perpendicular. That makes ∆ABC a right triangle with the right angle at A. The center of the circle must be (-3, -3), the midpoint of the hypotenuse. Surely you need no help seeing that its distance to each of the three given points is 1.
(x + 3)² + (y + 2)² = 1
Using the slopes, it is clear that lines AB and AC are perpendicular. That makes ∆ABC a right triangle with the right angle at A. The center of the circle must be (-3, -3), the midpoint of the hypotenuse. Surely you need no help seeing that its distance to each of the three given points is 1.
(x + 3)² + (y + 2)² = 1
2020-05-12 4:36 pm
The typical equation of a circle is: (x - xo)² + (y - yo)² = R² → where:
xo: abscissa of center
yo: ordinate of center
R: radius of circle
The circle passes through the point A (- 3 ; - 2), so these coordinates verify the equation of the circle.
(x - xo)² + (y - yo)² = R² → where: x = - 3 and where: y = - 2
(- 3 - xo)² + (- 2 - yo)² = R² ← memorize this result as (1)
The circle passes through the point B (- 2 ; - 3), so these coordinates verify the equation of the circle.
(x - xo)² + (y - yo)² = R² → where: x = - 2 and where: y = - 3
(- 2 - xo)² + (- 3 - yo)² = R² → recall (1): R² = (- 3 - xo)² + (- 2 - yo)²
(- 2 - xo)² + (- 3 - yo)² = (- 3 - xo)² + (- 2 - yo)²
4 + 4.xo + xo² + 9 + 6.yo + yo² = 9 + 6.xo + xo² + 4 + 4.yo + yo²
- 2.xo + 2.yo = 0
xo = yo ← memorize this result as (2)
The circle passes through the point C (- 4 ; - 3), so these coordinates verify the equation of the circle.
(x - xo)² + (y - yo)² = R² → where: x = - 4 and where: y = - 3
(- 4 - xo)² + (- 3 - yo)² = R² → recall (1): R² = (- 3 - xo)² + (- 2 - yo)²
(- 4 - xo)² + (- 3 - yo)² = (- 3 - xo)² + (- 2 - yo)²
16 + 8.xo + xo² + 9 + 6.yo + yo² = 9 + 6.xo + xo² + 4 + 4.yo + yo²
2.xo + 2.yo = - 12
xo + yo = - 6 → recall (2): xo = yo
xo + xo = - 6
2.xo = - 6
→ xo = - 3
Recall (2)
xo = yo → we know that: xo = - 3
→ yo = - 3
Recall (1)
(x - xo)² + (y - yo)² = R² → we know that: xo = yo = - 3
(x + 3)² + (y + 3)² = R² ← this is the equation of your circle
The circle passes through the point A (- 3 ; - 2), so these coordinates verify the equation of the circle.
(x + 3)² + (y + 3)² = R² → where: x = - 3 and where: y = - 2
(- 3 + 3)² + (- 2 + 3)² = R²
0 + 1 = R²
R = 1 ← the radius is 1
xo: abscissa of center
yo: ordinate of center
R: radius of circle
The circle passes through the point A (- 3 ; - 2), so these coordinates verify the equation of the circle.
(x - xo)² + (y - yo)² = R² → where: x = - 3 and where: y = - 2
(- 3 - xo)² + (- 2 - yo)² = R² ← memorize this result as (1)
The circle passes through the point B (- 2 ; - 3), so these coordinates verify the equation of the circle.
(x - xo)² + (y - yo)² = R² → where: x = - 2 and where: y = - 3
(- 2 - xo)² + (- 3 - yo)² = R² → recall (1): R² = (- 3 - xo)² + (- 2 - yo)²
(- 2 - xo)² + (- 3 - yo)² = (- 3 - xo)² + (- 2 - yo)²
4 + 4.xo + xo² + 9 + 6.yo + yo² = 9 + 6.xo + xo² + 4 + 4.yo + yo²
- 2.xo + 2.yo = 0
xo = yo ← memorize this result as (2)
The circle passes through the point C (- 4 ; - 3), so these coordinates verify the equation of the circle.
(x - xo)² + (y - yo)² = R² → where: x = - 4 and where: y = - 3
(- 4 - xo)² + (- 3 - yo)² = R² → recall (1): R² = (- 3 - xo)² + (- 2 - yo)²
(- 4 - xo)² + (- 3 - yo)² = (- 3 - xo)² + (- 2 - yo)²
16 + 8.xo + xo² + 9 + 6.yo + yo² = 9 + 6.xo + xo² + 4 + 4.yo + yo²
2.xo + 2.yo = - 12
xo + yo = - 6 → recall (2): xo = yo
xo + xo = - 6
2.xo = - 6
→ xo = - 3
Recall (2)
xo = yo → we know that: xo = - 3
→ yo = - 3
Recall (1)
(x - xo)² + (y - yo)² = R² → we know that: xo = yo = - 3
(x + 3)² + (y + 3)² = R² ← this is the equation of your circle
The circle passes through the point A (- 3 ; - 2), so these coordinates verify the equation of the circle.
(x + 3)² + (y + 3)² = R² → where: x = - 3 and where: y = - 2
(- 3 + 3)² + (- 2 + 3)² = R²
0 + 1 = R²
R = 1 ← the radius is 1
收錄日期: 2021-05-01 01:02:20
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200512061029AAEafhC



