Find [ (√3 + i)/2 ]⁶ + [ ( i - √3)/2 ]⁶ .?
2020-04-29 11:54 am
回答 (5)
2020-04-29 1:04 pm
✔ 最佳答案
I am using properties of imaginary quantities - 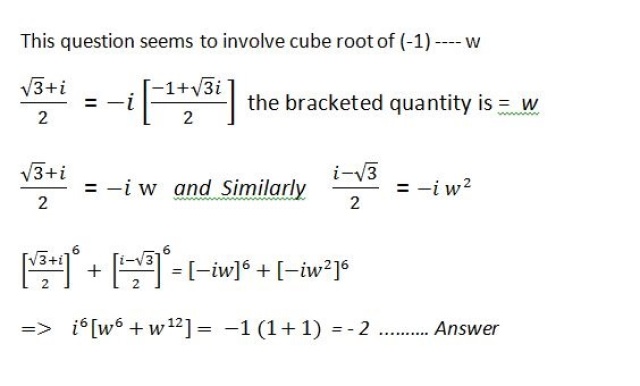
2020-04-29 12:46 pm
Refer to Pascal triangle below.
(x + y)⁶ = x⁶ + 6x⁵y + 15x⁴y² + 20x³y³ + 15x²y⁴ + 6xy⁵ + y⁶
(x - y)⁶ = x⁶ - 6x⁵y + 15x⁴y² - 20x³y³ + 15x²y⁴ - 6xy⁵ + y⁶
Hence, (x + y)⁶ + (x - y)⁶ = 2x⁶ + 30x⁴y² + 30x²y⁴ + 2y⁶
[(√3 + i)/2]⁶ + [(i - √3)/2]⁶
= [(√3 + i)⁶/2⁶] + [(√3 - i)⁶/2⁶]
= (1/64) × [(√3 + i)⁶ + (√3 - i)⁶]
= (1/64) × [2(√3)⁶ + 30(√3)⁴(i)² + 30(√3)²(i)⁴ + 2(i)⁶]
= (1/64) × [2(3)³ + 30(3)²(√-1)² + 30(3)(√-1)⁴ + 2(√-1)⁶]
= (1/64) × [54 - 270 + 90 - 2]
= (1/64) × (-128)
= -2
(x + y)⁶ = x⁶ + 6x⁵y + 15x⁴y² + 20x³y³ + 15x²y⁴ + 6xy⁵ + y⁶
(x - y)⁶ = x⁶ - 6x⁵y + 15x⁴y² - 20x³y³ + 15x²y⁴ - 6xy⁵ + y⁶
Hence, (x + y)⁶ + (x - y)⁶ = 2x⁶ + 30x⁴y² + 30x²y⁴ + 2y⁶
[(√3 + i)/2]⁶ + [(i - √3)/2]⁶
= [(√3 + i)⁶/2⁶] + [(√3 - i)⁶/2⁶]
= (1/64) × [(√3 + i)⁶ + (√3 - i)⁶]
= (1/64) × [2(√3)⁶ + 30(√3)⁴(i)² + 30(√3)²(i)⁴ + 2(i)⁶]
= (1/64) × [2(3)³ + 30(3)²(√-1)² + 30(3)(√-1)⁴ + 2(√-1)⁶]
= (1/64) × [54 - 270 + 90 - 2]
= (1/64) × (-128)
= -2

2020-04-29 1:16 pm
// Calculate [ (√3 + i)/2 ]⁶ + [ ( i - √3)/2 ]⁶ in 2 parts:
// Part 1: Calculate [ (√3 + i)/2 ]⁶
[ (√3 + i)/2 ]² = ¼ [3 + 2i√3 - 1] = ¼ [2 + 2i√3]
[ (√3 + i)/2 ]⁴ = [ (√3 + i)/2 ]² [ (√3 + i)/2 ]²
....................= ¼ [2 + 2i√3] ¼ [2 + 2i√3]
....................= ¹⁄₁₆ [2 + 2i√3]²
....................= ¹⁄₁₆ [4 + 8i√3 - 12]
....................= ¹⁄₁₆ [-8 + 8i√3]
[ (√3 + i)/2 ]⁶ = [ (√3 + i)/2 ]⁴ [ (√3 + i)/2 ]²
....................= ¹⁄₁₆ [-8 + 8i√3] ¼ [2 + 2i√3]
....................= ¹⁄₆₄ [-8 + 8i√3] [2 + 2i√3]
....................= ¹⁄₆₄ [-16 - 16i√3 + 16i√3 - 48]
....................= ¹⁄₆₄ [-16 - 48]
....................= ¹⁄₆₄ [-64]
....................= -1
// Part 2: Calculate [ ( i - √3)/2 ]⁶
[ ( i - √3)/2 ]² = ¼ [-1 - 2i√3 + 3] = ¼ [2 - 2i√3]
[ ( i - √3)/2 ]⁴ = [ ( i - √3)/2 ]² [ ( i - √3)/2 ]²
....................= ¼ [2 - 2i√3] ¼ [2 - 2i√3]
....................= ¹⁄₁₆ [2 - 2i√3]²
....................= ¹⁄₁₆ [4 - 8i√3 - 12]
....................= ¹⁄₁₆ [-8 - 8i√3]
[ ( i - √3)/2 ]⁶ = [ ( i - √3)/2 ]⁴ [ ( i - √3)/2 ]²
....................= ¹⁄₁₆ [-8 - 8i√3] ¼ [2 - 2i√3]
....................= ¹⁄₆₄ [-16 + 16i√3 - 16i√3 - 48]
....................= ¹⁄₆₄ [-16 - 48]
....................= ¹⁄₆₄ [-64]
....................= -1
// Finally combine the results from Part 1 and Part 2
[ (√3 + i)/2 ]⁶ + [ ( i - √3)/2 ]⁶ = -1 + (-1) = -2..................ANS
// Part 1: Calculate [ (√3 + i)/2 ]⁶
[ (√3 + i)/2 ]² = ¼ [3 + 2i√3 - 1] = ¼ [2 + 2i√3]
[ (√3 + i)/2 ]⁴ = [ (√3 + i)/2 ]² [ (√3 + i)/2 ]²
....................= ¼ [2 + 2i√3] ¼ [2 + 2i√3]
....................= ¹⁄₁₆ [2 + 2i√3]²
....................= ¹⁄₁₆ [4 + 8i√3 - 12]
....................= ¹⁄₁₆ [-8 + 8i√3]
[ (√3 + i)/2 ]⁶ = [ (√3 + i)/2 ]⁴ [ (√3 + i)/2 ]²
....................= ¹⁄₁₆ [-8 + 8i√3] ¼ [2 + 2i√3]
....................= ¹⁄₆₄ [-8 + 8i√3] [2 + 2i√3]
....................= ¹⁄₆₄ [-16 - 16i√3 + 16i√3 - 48]
....................= ¹⁄₆₄ [-16 - 48]
....................= ¹⁄₆₄ [-64]
....................= -1
// Part 2: Calculate [ ( i - √3)/2 ]⁶
[ ( i - √3)/2 ]² = ¼ [-1 - 2i√3 + 3] = ¼ [2 - 2i√3]
[ ( i - √3)/2 ]⁴ = [ ( i - √3)/2 ]² [ ( i - √3)/2 ]²
....................= ¼ [2 - 2i√3] ¼ [2 - 2i√3]
....................= ¹⁄₁₆ [2 - 2i√3]²
....................= ¹⁄₁₆ [4 - 8i√3 - 12]
....................= ¹⁄₁₆ [-8 - 8i√3]
[ ( i - √3)/2 ]⁶ = [ ( i - √3)/2 ]⁴ [ ( i - √3)/2 ]²
....................= ¹⁄₁₆ [-8 - 8i√3] ¼ [2 - 2i√3]
....................= ¹⁄₆₄ [-16 + 16i√3 - 16i√3 - 48]
....................= ¹⁄₆₄ [-16 - 48]
....................= ¹⁄₆₄ [-64]
....................= -1
// Finally combine the results from Part 1 and Part 2
[ (√3 + i)/2 ]⁶ + [ ( i - √3)/2 ]⁶ = -1 + (-1) = -2..................ANS
2020-04-29 12:29 pm
[ (√3 + i)/2 ]⁶ + [ ( i - √3)/2 ]⁶
Let's start out by taking the exponent of "6" and instead of applying it to the fractions, apply them to the numerator and denominator separately:
(√3 + i)⁶ / 2⁶ + (i - √3)⁶ / 2⁶
Now we can add the numerators:
[(√3 + i)⁶ + (i - √3)⁶] / 2⁶
Simplify the denominator:
[(√3 + i)⁶ + (i - √3)⁶] / 64
Now we'll start expanding the powers of 6. Let's turn that into the binomials squared, then cubed:
{[(√3 + i)²]³ + [(i - √3)²]³} / 64
Now square and simplify:
[(3 + 2i√3 + i²)³ + (i² - 2i√3 + 3)³] / 64
i² = -1, substiute and simplify:
[(3 + 2i√3 - 1)³ + (-1 - 2i√3 + 3)³] / 64
[(2 + 2i√3)³ + (2 - 2i√3)³] / 64
Now let's split up the cube into their products and start simplifying:
[(2 + 2i√3)(2 + 2i√3)(2 + 2i√3) + (2 - 2i√3)(2 - 2i√3)(2 - 2i√3)] / 64
[(4 + 4i√3 + 4i√3 + 4i² * 3)(2 + 2i√3) + (4 - 4i√3 - 4i√3 + 4i² * 3)(2 - 2i√3)] / 64
[(4 + 8i√3 + 12i²)(2 + 2i√3) + (4 - 8i√3 + 12i²)(2 - 2i√3)] / 64
i² = -1, again:
[(4 + 8i√3 - 12)(2 + 2i√3) + (4 - 8i√3 - 12)(2 - 2i√3)] / 64
[(-8 + 8i√3)(2 + 2i√3) + (-8 - 8i√3)(2 - 2i√3)] / 64
Multiply, substitute, and simplify one more time:
(-16 - 16i√3 + 16i√3 + 16i² * 3 - 16 + 16i√3 - 16i√3 + 16i² * 3) / 64
Now all of our i√3 terms cancel out:
(-16 + 16i² * 3 - 16 + 16i² * 3) / 64
(-16 + 48i² - 16 + 48i²) / 64
(-16 - 48 - 16 - 48) / 64
-128 / 64
-2
Let's start out by taking the exponent of "6" and instead of applying it to the fractions, apply them to the numerator and denominator separately:
(√3 + i)⁶ / 2⁶ + (i - √3)⁶ / 2⁶
Now we can add the numerators:
[(√3 + i)⁶ + (i - √3)⁶] / 2⁶
Simplify the denominator:
[(√3 + i)⁶ + (i - √3)⁶] / 64
Now we'll start expanding the powers of 6. Let's turn that into the binomials squared, then cubed:
{[(√3 + i)²]³ + [(i - √3)²]³} / 64
Now square and simplify:
[(3 + 2i√3 + i²)³ + (i² - 2i√3 + 3)³] / 64
i² = -1, substiute and simplify:
[(3 + 2i√3 - 1)³ + (-1 - 2i√3 + 3)³] / 64
[(2 + 2i√3)³ + (2 - 2i√3)³] / 64
Now let's split up the cube into their products and start simplifying:
[(2 + 2i√3)(2 + 2i√3)(2 + 2i√3) + (2 - 2i√3)(2 - 2i√3)(2 - 2i√3)] / 64
[(4 + 4i√3 + 4i√3 + 4i² * 3)(2 + 2i√3) + (4 - 4i√3 - 4i√3 + 4i² * 3)(2 - 2i√3)] / 64
[(4 + 8i√3 + 12i²)(2 + 2i√3) + (4 - 8i√3 + 12i²)(2 - 2i√3)] / 64
i² = -1, again:
[(4 + 8i√3 - 12)(2 + 2i√3) + (4 - 8i√3 - 12)(2 - 2i√3)] / 64
[(-8 + 8i√3)(2 + 2i√3) + (-8 - 8i√3)(2 - 2i√3)] / 64
Multiply, substitute, and simplify one more time:
(-16 - 16i√3 + 16i√3 + 16i² * 3 - 16 + 16i√3 - 16i√3 + 16i² * 3) / 64
Now all of our i√3 terms cancel out:
(-16 + 16i² * 3 - 16 + 16i² * 3) / 64
(-16 + 48i² - 16 + 48i²) / 64
(-16 - 48 - 16 - 48) / 64
-128 / 64
-2
2020-04-29 12:08 pm
[ (√3 + i)/2 ]⁶ + [ ( i - √3)/2 ]⁶ = -2
收錄日期: 2021-05-01 01:00:09
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200429035414AAbUbIj



