Maths!!!!! second degree equations ?
2020-04-14 9:48 pm
please answer with working out, guarantee 5 star
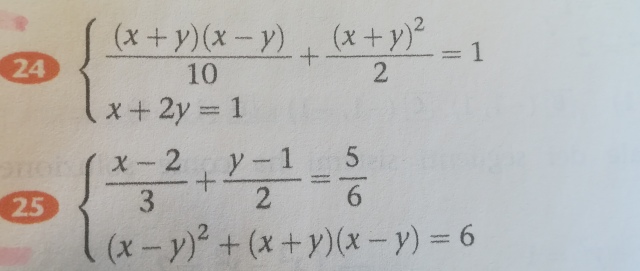
回答 (3)
2020-04-14 10:54 pm
✔ 最佳答案
24.[(x + y)(x - y)/10] + [(x + y)²/2] = 1 …… [1]
x + 2y = 1 …… [2]
[1] * 10:
{[(x + y)(x - y)/10] + [(x + y)²/2]} * 10 = 1 * 10
(x + y)(x - y) + 5(x + y)² = 10 …… [3]
From [2]:
x = 1 - 2y …… [4]
Plug [4] into [3]:
(1 - 2y + y)(1 - 2y - y) + 5(1 - 2y + y)² = 10
(1 - y)(1 - 3y) + 5(1 - y)² = 10
1 - 4y + 3y² + 5 - 10y + 5y² = 10
8y² - 14y -4 = 0
2(y - 2)(4y + 1) = 0
y = 2 or y = -1/4
Plug y = 2 into [4]:
x = 1 - 2(2)
x = -3
Plug y = -1/4 into [4]
x = 1 - 2(-1/4)
x = 3/2
Hence, (x, y) = (-3, 2) or (3/2, -1/4)
====
25.
[(x - 2)/3] + [(y - 1)/2] = 5/6 …… [1]
(x - y)² + (x + y)(x - y) = 6 …… [2]
[1] * 6:
{[(x - 2)/3] + [(y - 1)/2]} * 6 = (5/6) * 6
2(x - 2) + 3(y - 1) = 5
2x - 4 + 3y - 3 = 5
2x = 12 - 3y …… [3]
[2] * 4:
{(x - y)² + (x + y)(x - y)} * 4 = 6 * 4
(2x - 2y)² + (2x + 2y)(2x - 2y) = 24 …… [4]
Plug [3] into [4]:
(12 - 3y - 2y)² + (12 - 3y + 2y)(12 - 3y - 2y) = 24
(12 - 5y)² + (12 - y)(12 - 5y) = 24
144 - 120y + 25y² + 144 - 72y + 5y² = 24
30y² - 192y + 264 = 0
6(x - 2)(5y - 22) = 0
y = 2 or y = 22/5
Plug y = 2 into [3]:
2x = 12 - 3(2)
2x = 6
x = 3
Plug y = 22/5 into [3]:
2x = 12 - 3(22/5)
2x = -6/5
x = -3/5
Hence, (x, y) = (3, 2) or (-3/5, 22/5)
2020-04-14 11:16 pm
24).
((x + y)(x - y) + 5(x + y)^2 = 10
x + 2y = 1
Solutions:
x = -3, y = 2
x = 3/2, y = -1/4
25).
2(x - 2) + 3(y - 1) = 5
(x - y)^2 + (x + y)(x - y) = 6
Solutions:
x = -3/5, y = 22/5
x = 3, y = 2
((x + y)(x - y) + 5(x + y)^2 = 10
x + 2y = 1
Solutions:
x = -3, y = 2
x = 3/2, y = -1/4
25).
2(x - 2) + 3(y - 1) = 5
(x - y)^2 + (x + y)(x - y) = 6
Solutions:
x = -3/5, y = 22/5
x = 3, y = 2
2020-04-14 10:16 pm
I'll try one
multiply by 10
(x+y)(x–y) + 5(x+y)² = 10
(x+y)(x–y) + 5(x+y)(x+y) = 10
(x+y)((x–y) + 5(x+y)) = 10
(x+y)(x–y + 5x+5y) = 10
(x+y)(6x+4y) = 10
x+2y = 1
x = 1–2y
(x+y)(6x+4y) = 10
(1–2y+y)(6(1–2y)+4y) = 10
(1–y)(6–12y+4y) – 10 = 0
(1–y)(6–8y) – 10 = 0
6–8y–6y+8y²–10 = 0
8y² – 14y – 4 = 0
4y² – 7y – 2 = 0
y = 2, –1/4
for y=2, x = 1–2y = –3
for y=–1/4, x = 1–2(–1/4) = 1+1/2 = 3/2
check –3,2
(x+y)(x–y) + 5(x+y)² = 10
(–3+2)(–3–2) + 5(–3+2)² = 10
(–1)(–5) + 5(–1)² = 10
5 + 5 = 10
x+2y = 1
–3+4 = 1
check 3/2,–14
you can do that...
multiply by 10
(x+y)(x–y) + 5(x+y)² = 10
(x+y)(x–y) + 5(x+y)(x+y) = 10
(x+y)((x–y) + 5(x+y)) = 10
(x+y)(x–y + 5x+5y) = 10
(x+y)(6x+4y) = 10
x+2y = 1
x = 1–2y
(x+y)(6x+4y) = 10
(1–2y+y)(6(1–2y)+4y) = 10
(1–y)(6–12y+4y) – 10 = 0
(1–y)(6–8y) – 10 = 0
6–8y–6y+8y²–10 = 0
8y² – 14y – 4 = 0
4y² – 7y – 2 = 0
y = 2, –1/4
for y=2, x = 1–2y = –3
for y=–1/4, x = 1–2(–1/4) = 1+1/2 = 3/2
check –3,2
(x+y)(x–y) + 5(x+y)² = 10
(–3+2)(–3–2) + 5(–3+2)² = 10
(–1)(–5) + 5(–1)² = 10
5 + 5 = 10
x+2y = 1
–3+4 = 1
check 3/2,–14
you can do that...
收錄日期: 2021-04-24 07:48:37
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200414134824AARgeuU
