Calculus max and min values ?

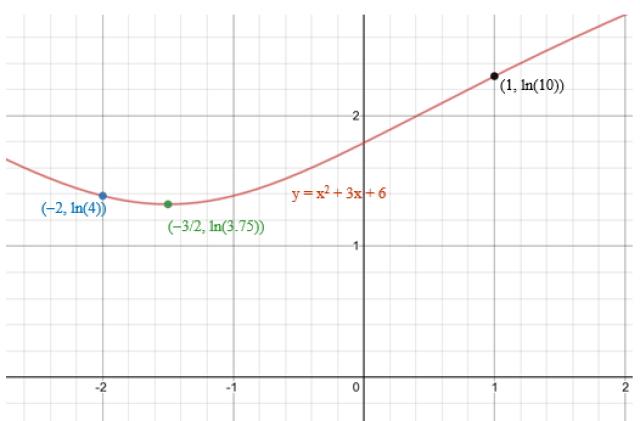
f(x) = ln(x² + 3x + 6)

f'(x) = (2x + 3) / (x² + 3x + 6)
Relative maximum/minimum at x = -3/2

f(-3/2) = ln[(-3/2)² + 3(-3/2) + 6] = ln(3.75)
f(-2) = ln[(-2)² + 3(-2) + 6] = ln(4)
f(1) = ln[(1)² + 3(1) + 6] = ln(10)

ln(10) > ln(4) > ln(3.75)

Maximum value of f = ln(10) at x = 1
Minimum value of f = ln(3.75) at x = -3/2

⊳ Absolute min/Max will exist for the Weirestrass theorem

⊳ Absolute min/Max points has to be searched among singular points, critical points and border points.
1. Domain=[-2,1]f(x) is defined, continuous and differentiable in all points of [-2,1].i) No singular points. It is differentiableii) Critical or stationary pointsfirst derivative f '(x)=(2x+3)/(x^2+3x+6)critical points f '(x)=0 ⇒ 2x+3=0 ⇒ x-3/2 where f(x) takes on value f(-3/2) = log(15/4)iii) border pointsf(-2) = log(4)f(1) = log(10)Comparing the results, we can conclude:• Absolute minimun value is f(x)=log(15/4) for x=-3/2• Absolute massimun value is f(x)=log(10) for x=1