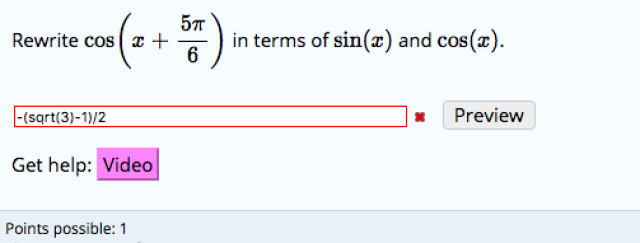
Sum and Difference Identities?
回答 (7)
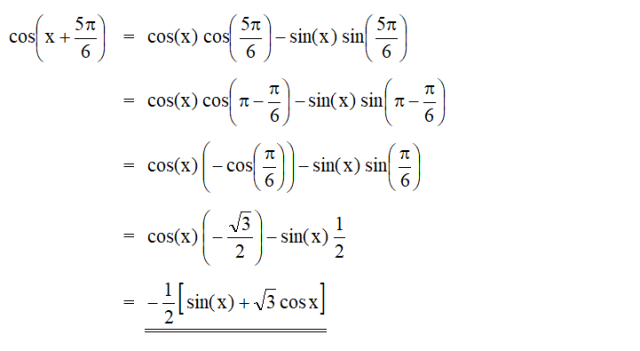
2020-04-03 5:19 pm
Put (5pi/6) = y. Now cos(x+y) = cosx*cosy - sinx*siny and (5pi/6) = pi - pi/6.
Then cosy = cos(pi-pi/6) = -cos(pi/6) = -(1/2)rt3;
and siny = sin(pi-pi/6) = sin(pi/6) = (1/2).
Then cos[x+(5pi/6)] = -(1/2)rt3*cosx - (1/2)*sinx = - (1/2)[rt3*cosx + sinx].
Then cosy = cos(pi-pi/6) = -cos(pi/6) = -(1/2)rt3;
and siny = sin(pi-pi/6) = sin(pi/6) = (1/2).
Then cos[x+(5pi/6)] = -(1/2)rt3*cosx - (1/2)*sinx = - (1/2)[rt3*cosx + sinx].
2020-04-05 11:45 pm
cos (x + 5π/6)
= -cos(π/6 - x)
= -sin(x)/2 - 1/2 sqrt(3) cos(x)
= -cos(π/6 - x)
= -sin(x)/2 - 1/2 sqrt(3) cos(x)
2020-04-03 9:31 pm
cos(x+5pi/6)=
cos(x)cos(5pi/6)-sin(x)sin(5pi/6)=
-cos(x)cos(pi/6)-sin(x)sin(pi/6)=
-[sqr(3)cos(x)+sin(x)]/2
cos(x)cos(5pi/6)-sin(x)sin(5pi/6)=
-cos(x)cos(pi/6)-sin(x)sin(pi/6)=
-[sqr(3)cos(x)+sin(x)]/2
2020-04-03 3:26 pm
cos(A + B) => cosAcosB - sinAsinB
so, cos(x + 5π/6) => cos(x)cos(5π/6) - sin(x)sin(5π/6)
Now, cos(5π/6) = -√3/2 and sin(5π/6) = 1/2
Hence, cos(x + 5π/6) => (-√3/2)cosx - (1/2)sinx
i.e. (-1/2)(√3cosx + sinx)
:)>
so, cos(x + 5π/6) => cos(x)cos(5π/6) - sin(x)sin(5π/6)
Now, cos(5π/6) = -√3/2 and sin(5π/6) = 1/2
Hence, cos(x + 5π/6) => (-√3/2)cosx - (1/2)sinx
i.e. (-1/2)(√3cosx + sinx)
:)>
2020-04-03 3:00 pm
(-√3/2)cosx - (1/2)sinx
2020-04-03 2:38 pm
stop doing this to us please
收錄日期: 2021-05-01 01:05:53
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20200403062901AAYJtso