Maths problem: how to do, thanks?

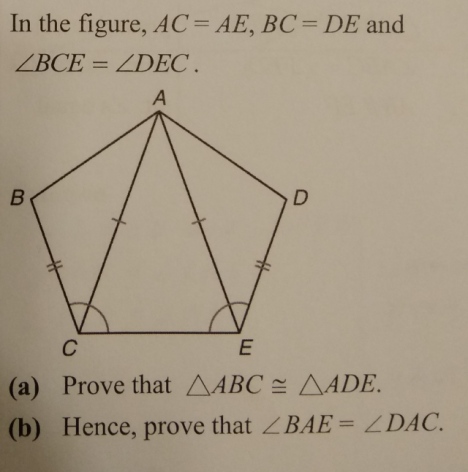
(a) AC=AE 　　(given)
∴ △ACE is an isos.△
=> ∠ACE=∠AEC . . . . . . . . . . . . . ①

Now, 　　　　∠BCE=∠DEC 　　(given)
i.e.　　∠ACB+∠ACE=∠AED+∠AEC
Hence,from①: ∠ACB=∠AED ------------- (#)

Also, given that :AC=AE, BC=DE -------- (##)

From (#) & (##), △ABC≅△ADE (SAS) 

(b)
From (a) : ∠BAC=∠DAE (corr.∠s, ≅△s)
So,∠BAC+∠CAE=∠DAE+∠CAE
i.e. 　　　 ∠BAE=∠DAC

AC = AE.
∴ ∠ACE = ∠AEC,
∴∠ACB = ∠AED
依 SAS 定理, △ABC 全等 △ADE.
∴ ∠ABC = ∠ADE,
   ∠BAC = ∠DAE.
∴ ∠BAE = ∠DAC