Maths problem, how to do thanks?
2019-05-29 11:22 am
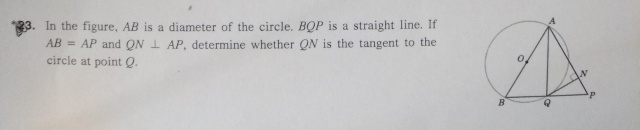
回答 (1)
2019-05-29 12:58 pm
✔ 最佳答案
Solution (REVISED) :===============
∵ AB=AP, ∴△BAP is an isosceles △
=> ∠ABP=∠APB
Let ∠ABP=∠APB = b
From △ABQ,
∠AQB=90⁰ (∠ in semicircle)
∴ ∠BAQ = 90⁰ - b . . . . . . . . . . . . . ①
From △PQN,
∠QNP=90⁰ (Given that QN丄AP)
∴ ∠PQN = 90⁰ - b . . . . . . . . . . . . . ②
①&② : ∠BAQ = ∠PQN . . . . . . . . . . . . . (#)
Now, from △ABQ, ∠ABQ = 90⁰ - ∠BAQ. . . . . . . . . . . ③
Also, from pt. Q, ∠AQN = 90⁰ - ∠PQN. . . . . . . . . . . . .④
Concluding from (#), ③&④ : ∠ABQ = ∠AQN
Conclusion :
QN is tangent to the circle at Q (converse of ∠ in alternate segment)
收錄日期: 2021-04-24 07:32:16
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20190529032236AAoOsrF

