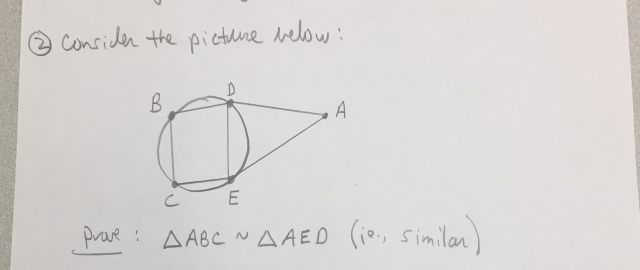
How can I prove that ABC and AED are not similar?

What is given? For example, is BCED a specific quadrilateral (square, rectangle)?

If it can be any arbitrary quadrilateral, I could make it so ABC and AED *are* similar.

You request is most confusing. What you ask to prove is in direct conflict with what is asked in the attached image. No clear conditions are given. Consider these conditions:

Points A, D, and B are collinear.
Points A, E, and C are collinear.
Quadrilateral BCED is a cyclic quadrilateral.

If all three of those conditions are true, then ∆ABC ~ ∆AED. However, the first two conditions appear to be in conflict with your sketch.

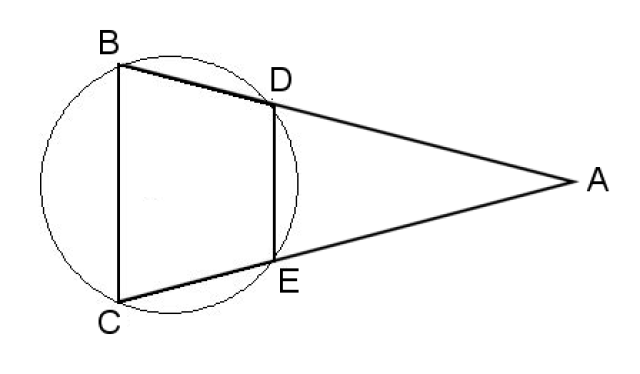
Look at the picture ..
B and C are on the opposite side of the circle to A
D and E are on the same side of the circle to A
So ..
ADE is a triangle .. but the shape ABC is the triangle ADE stuck on the side of the square CBDE
Not similar at all.

Or are ADB and AEC meant to be straight lines ?