u = cos x
du/dx = -sinx
du= -sin dx
du/-sinx = dx
therefore, INT sin^3(x) u^3 du/-sinx
cancels to: INT -sin^2(x) u^3 du
[-sin^2(x) = u^2 - 1] so becomes:
INT (u^2 - 1)u^3 du
= INT (u^5 - u^3) du
== 1/6 u^6 - 1/4 u^4
=== 1/6 cos^6(x) - 1/4 cos^4(x) +c
Can you integrate sin^3(x)cos^3(x) dx this way...?
2019-02-26 7:01 pm
回答 (3)
2019-02-26 10:07 pm
sin^3(x)cos^3(x) dx = (sin x cos x)^3= (1/2 sin 2x)^3
1/8 sin 2x sin^2x= 1/8 sin 2x (1-cos^2x)
=1/8 sin 2x - 1/8 sin 2x cos^2x
Integrate now .
=1/8 (-cos 2x) 1/2 -1/8 (-1/3 cos^3 (2x) +c
= 1/24 cos^3 (2x) -1/16 cos 2x +c
This seem to be the answer.
1/8 sin 2x sin^2x= 1/8 sin 2x (1-cos^2x)
=1/8 sin 2x - 1/8 sin 2x cos^2x
Integrate now .
=1/8 (-cos 2x) 1/2 -1/8 (-1/3 cos^3 (2x) +c
= 1/24 cos^3 (2x) -1/16 cos 2x +c
This seem to be the answer.
2019-02-26 7:49 pm
That seems like the most straightforward way to me.
Also used here
https://www.integral-calculator.com/#expr=sin%5E3xcos%5E3x
(Choose "substitue cosx" option, but same thing either way)
Also used here
https://www.integral-calculator.com/#expr=sin%5E3xcos%5E3x
(Choose "substitue cosx" option, but same thing either way)
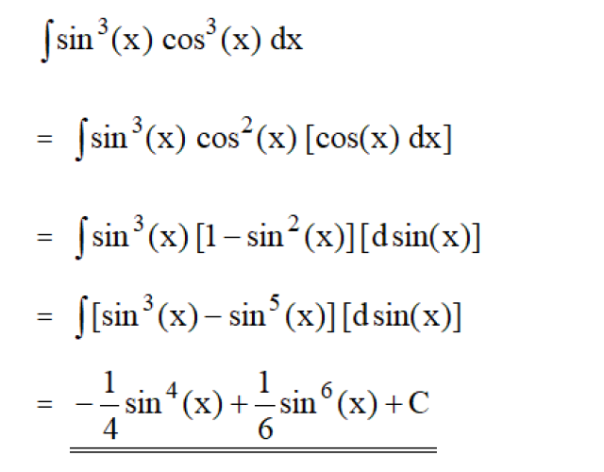
收錄日期: 2021-05-01 22:28:29
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20190226110126AApdFvV