更新1:
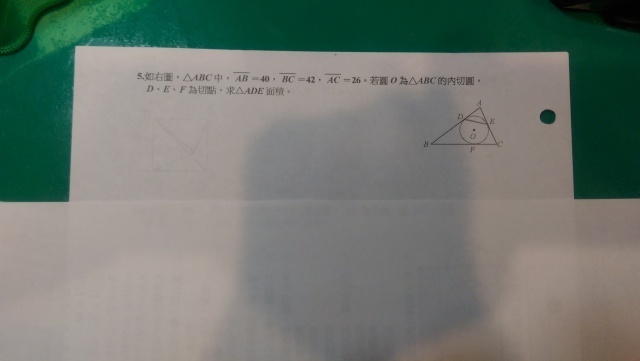
三角形ABC的面積是504 但是題目是問三角形ADE 若不用三角函數,可有方法解題嗎? 謝謝 螞蟻雄兵大師
如附圖 請問三角形ADE的面積是多少?
回答 (1)
2018-11-27 1:10 pm
✔ 最佳答案
設AD=x =>AE=x
且 BD=40 - x 和 CE=26 - x
=> BF=40 - x 和 CF=26 - x
∴ (40 - x) + (26 - x) = 42 - - - -→ { ∵ BF+CF = BC
66-2x = 42
∴ x = 12
連接 C,D 成 CD
從△ACB, m△ACD : m△ACB = 12 : 40 -→{m△ACD代表△ACD面積
m△ACD : 504 = 12 : 40
∴ m△ACD = 756/5
從△ACD, m△AED : m△ACD = 12 : 26
m△AED : 756/5 = 12 : 26
∴ m△AED = 4536/65
________________________ 完 ________________________
# : A
. . . . . / | \
. . . . /. .|. . \
. . . /. . .|. . . .\
. . /. . . .| h. . . .\
. ./. . . . |. . . . . . \
./_____|_______\
B<---->D<-------->C
2018-11-26 4:08 pm
Sol
設AD=x
BD=40－X
BF=40－x
CF=42－(40－x)=x+2
CE=x+2
AE=x
AE+CE=26
x+(x+2)=26
x=12
CosA=(40^2+26^2－42^2)/(2*40*26)=512/2080=16/65
SinA=63/65
△ADE=(1/2)*12*12*(63/65)=4536/65
Sol
設AD=x，半徑=r
BD=40－X
BF=40－x
CF=42－(40－x)=x+2
CE=x+2
AE=x
AE+CE=26
x+(x+2)=26
x=12
s=(40+42+26)/2=54
△ABC=√[54*(54-40)*(54-42)*(54-26)]=√254016=504
△ABC=504*/[12*12/(40*26)]=4536/65
設AD=x
BD=40－X
BF=40－x
CF=42－(40－x)=x+2
CE=x+2
AE=x
AE+CE=26
x+(x+2)=26
x=12
CosA=(40^2+26^2－42^2)/(2*40*26)=512/2080=16/65
SinA=63/65
△ADE=(1/2)*12*12*(63/65)=4536/65
Sol
設AD=x，半徑=r
BD=40－X
BF=40－x
CF=42－(40－x)=x+2
CE=x+2
AE=x
AE+CE=26
x+(x+2)=26
x=12
s=(40+42+26)/2=54
△ABC=√[54*(54-40)*(54-42)*(54-26)]=√254016=504
△ABC=504*/[12*12/(40*26)]=4536/65
收錄日期: 2021-04-30 22:54:00
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20181126060603AA6wbYF