Solving the equation?

sqrt(((x - 5)^2) + (y^2)) - sqrt(((x + 5)^2) + (y^2)) = 6;

sqrt(((x - 5)^2) + (y^2)) = sqrt(((x + 5)^2) + (y^2)) + 6;

((x - 5)^2) + (y^2) = 36 + ((x + 5)^2) + (y^2) + 12*sqrt(((x + 5)^2) + (y^2));

(x - 5)^2 = 36 + ((x + 5)^2) + 12*sqrt(((x + 5)^2) + (y^2));

(x^2) - 10x + 25 = 36 + (x^2) + 10x + 25 + 12*sqrt(((x + 5)^2) + (y^2));

-10x = 36 + 10x + 12*sqrt(((x + 5)^2) + (y^2));

-20x = 36 + 12*sqrt(((x + 5)^2) + (y^2));

-36 - 20x = 12*sqrt(((x + 5)^2) + (y^2));

-5x - 9= 3*sqrt(((x + 5)^2) + (y^2));

(5x + 9)^2 = 9*(((x + 5)^2) + (y^2));

25*(x^2) + 90x + 81 = 9*((x^2) + 10x + 25 + (y^2));

25*(x^2) + 90x + 81 = 9*(x^2) + 90x + 225 + 9*(y^2);

25*(x^2) + 81 = 9*(x^2) + 225 + 9*(y^2);

16*(x^2) + 81 = 225 + 9*(y^2);

16*(x^2) - 9*(y^2) = 144;

You've told us ... it's 6

sqrt root of [(x-5)^2 + y^2] - sqrt root of [(x+5)^2 + y^2] = 6
=== answer
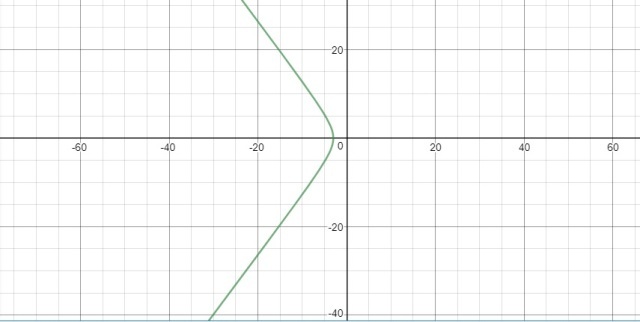
The answer is this is actually a curve and has multiple (infinite solutions) Half of an hyperbola like curve.
The vertex is and one solution is (-3,0)
checking
sqrt( (-3-5)^2 + 0 ) - sqrt( (-3+5)^2 +)) = 6
sqrt( -8^2 ) - sqrt( (-2)^2) = 6
8 - 2 = 6