Find the eqn of tangents from origin to the circle x²+y²-6x+2=0?

As the tangent passes through the origin, the y-intercept of the tangent is 0.
Let y = mx be the tangent from the origin to the circle.

Substitute y = mx into the equation of the circle.
x² + (mx)²- 6x + 2 = 0
(1 + m²)x² - 6x + 2 = 0

As there is one point of intersection, the above equation has only one root, and thus discriminant, Δ = 0
6² - 4*(1 +m²)*2 = 0
36 - 8 - 8m² = 0
8m² = 28
2m² = 7
m² = 7/2
m = ±√(7/2)

The equation of the tangent is: y = ±√(7/2) x

(±√(7/2) x ≠ ± √(7x/2). The given answer is incorrect.)

　
First we find dy/dx for circle using implicit differentiation:

x² + y² − 6x + 2 = 0
2x + 2y dy/dx − 6 = 0
2y dy/dx = 6 − 2x
dy/dx = (3−x)/y

Now we must find point(s) (x,y) on circle such that slope from (0,0) to (x,y) = dy/dx

(y−0)/(x−0) = (3−x)/y
y/x = (3−x)/y
y² = 3x−x²

Substitute this value of y² into equation of circle and solve for x:

x² + y² − 6x + 2 = 0
x² + (3x−x²) − 6x + 2 = 0
−3x = −2
x = 2/3

y² = 3x−x² = 2−4/9 = 14/9
y = ± √14/3

Points of tangency are (2/3, ±√14/3)

Since tangents pass through origin, they have equation y = mx, where m = slope
m = (± √14/3)/(2/3) = ± √14/2 = ± √(7/2)

Tangent lines:

y = ± √(7/2) x

NOTE: x should NOT be under square root as you've shown.

As I write, you have two correct solutions using very different methods. Allow me to contribute one more look. This is pretty much how I would construct the two tangent lines were it a geometry construction problem.

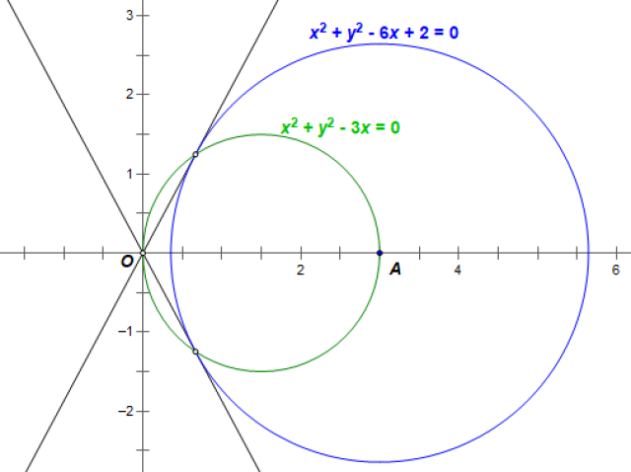
Let the center of the given circle be A(3, 0), while O(0, 0) is the origin.

The circle with diameter OA:

(x - 0)(x - 3) + (y - 0)(y - 0) = 0
x² + y² - 3x = 0

This circle intersects the given circle at the two points of tangency.

x² + y² - 6x + 2= 0
x² + y² - 3x = 0 (-)
----------------------
-3x + 2 = 0
x = 2/3

(2/3)² + y² - 3(2/3) = 0
y² = 14/9
y = ±√(14)/3

The points of tangency are (2/3, √(14)/3) and (2/3, -√(14)/3).

corresponding slopes = ±[√(14)/3] / (2/3) = ±√(14)/2

The tangent lines:

7x + √(14)y = 0
7x - √(14)y = 0

Slope of tangent y = mx is given by
2x + 2y*m – 6 = 0
y = [(3 – x)/y]x, so substitute y^2 = 3x – x^2
x^2 – 6x + 3x – x^2 + 2 = 0
The two tangent points share x = 2/3
y^2 = (2/3)*(7/3), so y = ±√(14)/3
Tangent lines are y = ±[√(14)/2]x

https://www.wolframalpha.com/input/?i=x%5E2+%2B+y%5E2+-+6x+%2B+2+%3D+0,+y+%3D+%5B%E2%88%9A(14)%2F2%5Dx,+y+%3D+-+%5B%E2%88%9A(14)%2F2%5Dx

2x+2yy' = 6
dy/dx = (3-x)/y =