How many students take two subjects only?

M stands for Math.
E stands for Eng.
P stands for Phy.

n(M) + n(E) + n(P) = n(M∪E∪P) + n(M∩E) + n(M∩P) + n(P∩E) - n(M∩E∩P)
35 + 32 + 40 = 64 + 17 + 15 + 12 - n(M∩E∩P)
n(M∩E∩P) = 64 + 17 + 15 + 12 - 35 - 32 - 40
n(M∩E∩P) = 1
n(M∩E∩P) = 1

Number of students taking two subjects only
= n(M∩E) + n(M∩P) + n(P∩E) - 3n(M∩E∩P)
= 17 + 15 + 12 - 3×1
= 41

====
Check:
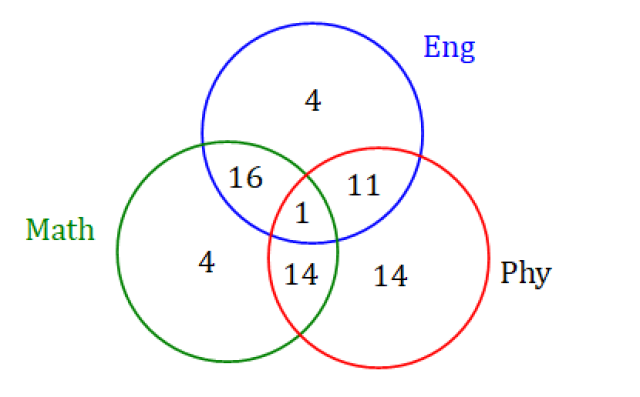
Refer to the diagram below:
Total number of students = 4 + 16 + 1 + 11 + 4 + 14 + 14 = 64
Number of students taking Math = 4 + 16 + 1 + 14 = 35
Number of students taking Eng = 4 + 16 + 1 + 11 = 32
Number of students taking Phy = 1 + 11 + 14 + 14 = 40
Number of students taking both Math & Eng = 16 + 1 = 17
Number of students taking both Math & Phy = 1 + 14 = 15
Number of students taking both Phy & Eng = 1 + 11 = 12
Number of students taking 2 subjects = 16 + 11 + 14 = 41