find the intergral of cos(lnx) dx?
2018-05-19 10:22 pm
回答 (5)
2018-05-19 10:53 pm
The answer is as follows :
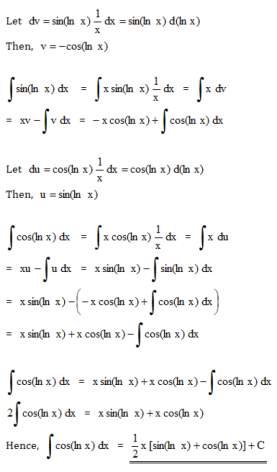
2018-05-19 11:04 pm
Use Complex numbers
cos(u) = (e^(iu) + e(-iu))/2
sin(u) = (e^(iu) - e(-iu))/2i = (ie(-iu) - ie^(iu))/2
so cos(ln(x)) = (x^i + x^-i)/2
and sin(ln(x)) = (ix^-i - ix^i)/2
integrate: (x^(i+1)/(i+1) + x^(1-i)/(1-i))/2 + C
combine fractions: ((1-i)x^(i+1)+(i+1)x^(1-i))/(2*(i+1)(1-i)) + C
x(-ix^i + ix^-i + x^i + x^-i)/4 + C
x(cos(ln(x))+sin(ln(x)))/2 + C
Now we check
cos(ln(x))/2 - sin(ln(x))/2 + sin(ln(x))/2 + cos(ln(x))/2 = cos(ln(x))
Alternatively using substitution and integration by parts
let u= ln(x)
du = 1/x dx
x du = dx
e^u du = dx
so integrate e^u*cos(u) du
Integrate by parts, f(u) = e^u, g'(u) = cos(u)
f'(u) = e^u, g(u) = sin(u)
so e^u*cos(u) du = e^u*sin(u) - (e^u*sin(u) du) + C
Integrate by parts again, f2(u) = e^u, g2'(u) = sin(u)
f2'(u) = e^u, g2(u) = -cos(u)
so e^u*cos(u) du = e^u*sin(u) - (e^u*sin(u) du) + C = e^u*sin(u) + e^u*cos(u) - (e^u*cos(u) du) + C
Collect the integrals
2*e^u*cos(u) du = e^u*sin(u) + e^u*cos(u) + C
e^u*cos(u) du = e^u(sin(u) + cos(u))/2 + C
Resubstitute u = ln(x)
x(sin(ln(x)) + cos(ln(x)))/2 + C
Same Answer.
cos(u) = (e^(iu) + e(-iu))/2
sin(u) = (e^(iu) - e(-iu))/2i = (ie(-iu) - ie^(iu))/2
so cos(ln(x)) = (x^i + x^-i)/2
and sin(ln(x)) = (ix^-i - ix^i)/2
integrate: (x^(i+1)/(i+1) + x^(1-i)/(1-i))/2 + C
combine fractions: ((1-i)x^(i+1)+(i+1)x^(1-i))/(2*(i+1)(1-i)) + C
x(-ix^i + ix^-i + x^i + x^-i)/4 + C
x(cos(ln(x))+sin(ln(x)))/2 + C
Now we check
cos(ln(x))/2 - sin(ln(x))/2 + sin(ln(x))/2 + cos(ln(x))/2 = cos(ln(x))
Alternatively using substitution and integration by parts
let u= ln(x)
du = 1/x dx
x du = dx
e^u du = dx
so integrate e^u*cos(u) du
Integrate by parts, f(u) = e^u, g'(u) = cos(u)
f'(u) = e^u, g(u) = sin(u)
so e^u*cos(u) du = e^u*sin(u) - (e^u*sin(u) du) + C
Integrate by parts again, f2(u) = e^u, g2'(u) = sin(u)
f2'(u) = e^u, g2(u) = -cos(u)
so e^u*cos(u) du = e^u*sin(u) - (e^u*sin(u) du) + C = e^u*sin(u) + e^u*cos(u) - (e^u*cos(u) du) + C
Collect the integrals
2*e^u*cos(u) du = e^u*sin(u) + e^u*cos(u) + C
e^u*cos(u) du = e^u(sin(u) + cos(u))/2 + C
Resubstitute u = ln(x)
x(sin(ln(x)) + cos(ln(x)))/2 + C
Same Answer.
2018-05-20 1:53 am
int cos(ln(x)) dx;
Let x = e^t; dx = e^t dt;
int cos(t)*(e^t) dt;
u = cos(t); du = -sin(t) dt; dv = e^t dt; v = e^t dt;
cos(t)*(e^t) + int (e^t)*sin(t) dt;
u = sin(t); du = cos(t) dt; dv = e^t dt; v = e^t dt;
cos(t)*(e^t) + sin(t)*(e^t) - int (e^t)*cos(t) dt = int cos(t)*(e^t) dt;
cos(t)*(e^t) + sin(t)*(e^t) = 2 * int cos(t)*(e^t) dt;
(e^t)*(cos(t) + sin(t))/2 = int cos(t)*(e^t) dt;
int cos(ln(x)) dx = (x*(cos(ln(x)) + sin(ln(x)))/2) + C
Let x = e^t; dx = e^t dt;
int cos(t)*(e^t) dt;
u = cos(t); du = -sin(t) dt; dv = e^t dt; v = e^t dt;
cos(t)*(e^t) + int (e^t)*sin(t) dt;
u = sin(t); du = cos(t) dt; dv = e^t dt; v = e^t dt;
cos(t)*(e^t) + sin(t)*(e^t) - int (e^t)*cos(t) dt = int cos(t)*(e^t) dt;
cos(t)*(e^t) + sin(t)*(e^t) = 2 * int cos(t)*(e^t) dt;
(e^t)*(cos(t) + sin(t))/2 = int cos(t)*(e^t) dt;
int cos(ln(x)) dx = (x*(cos(ln(x)) + sin(ln(x)))/2) + C
2018-05-20 2:14 am
∫ cos(ln x) dx
Let t= ln(x); dt = 1/x dx
x=e^t
∫ cos(ln x) dx = ∫ e^t cos(t) dt
Let I = ∫ e^t cos(t) dt
Integrate by parts
dv= e^t dt; v=e^t
u = cos(t); du = -sin(t) dt
∫ u dv = uv - ∫ v du
I = cos(t) e^t - ∫ e^t (-sin (t)) dt
I = e^t cos(t) + ∫ e^t sin(t) dt ------------(1)
Integrate ∫ e^t sin(t) dt by parts
dv= e^t dt ; v=e^t
u = sin(t); du =cos(t) dt
∫ u dv = uv - ∫ v du
∫ e^t sin(t) dt = e^t sin(t) - ∫ e^t cos(t) dt
∫ e^t sin(t) dt = e^t sin(t) - I
substitute this into (1) for ∫ e^t sin(t) dt
I = e^t cos(t) + e^t sin(t) - I
2I = e^t (cos(t)+sin(t))
I = (1/2) e^t ( cos(t) + sin(t) )
replace t by ln x
= (1/2) e^ln x (cos(ln x) + sin(ln x) )
= (1/2) x (cos(ln x) + sin(ln x) ) + C
Let t= ln(x); dt = 1/x dx
x=e^t
∫ cos(ln x) dx = ∫ e^t cos(t) dt
Let I = ∫ e^t cos(t) dt
Integrate by parts
dv= e^t dt; v=e^t
u = cos(t); du = -sin(t) dt
∫ u dv = uv - ∫ v du
I = cos(t) e^t - ∫ e^t (-sin (t)) dt
I = e^t cos(t) + ∫ e^t sin(t) dt ------------(1)
Integrate ∫ e^t sin(t) dt by parts
dv= e^t dt ; v=e^t
u = sin(t); du =cos(t) dt
∫ u dv = uv - ∫ v du
∫ e^t sin(t) dt = e^t sin(t) - ∫ e^t cos(t) dt
∫ e^t sin(t) dt = e^t sin(t) - I
substitute this into (1) for ∫ e^t sin(t) dt
I = e^t cos(t) + e^t sin(t) - I
2I = e^t (cos(t)+sin(t))
I = (1/2) e^t ( cos(t) + sin(t) )
replace t by ln x
= (1/2) e^ln x (cos(ln x) + sin(ln x) )
= (1/2) x (cos(ln x) + sin(ln x) ) + C
2018-05-19 10:30 pm
收錄日期: 2021-04-24 01:04:37
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20180519142208AA8zxZ1
