3.L.1 Find dy/dx using logarithmic differentiation.
y = x sqrt(x2 + 7) , x > 0
Find dy/dx using logarithmic differentiation.?
2018-04-08 10:09 pm
回答 (6)
2018-04-09 5:32 am
✔ 最佳答案
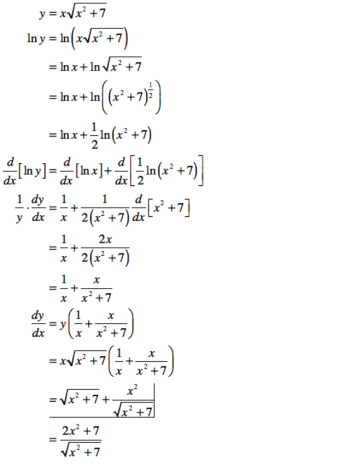
2018-04-08 10:29 pm
y = x √(x² + 7)
log(y) = log[x √(x² + 7)]
log(y) = log(x) + log√(x² + 7)
log(y) = log(x) + (1/2)log(x² + 7)
(d/dx)[log(y)] = (d/dx)[log(x) + (1/2)log(x² + 7)]
(1/y)(dy/dx) = (1/x) + [1/2(x² + 7)]•(d/dx)(x² + 7)
(1/y)(dy/dx) = (1/x) + [x/(x² + 7)]
(dy/dx) = y {(1/x) + [x/(x² + 7)]}
(dy/dx) = [x √(x² + 7)] {(1/x) + [x/(x² + 7)]}
log(y) = log[x √(x² + 7)]
log(y) = log(x) + log√(x² + 7)
log(y) = log(x) + (1/2)log(x² + 7)
(d/dx)[log(y)] = (d/dx)[log(x) + (1/2)log(x² + 7)]
(1/y)(dy/dx) = (1/x) + [1/2(x² + 7)]•(d/dx)(x² + 7)
(1/y)(dy/dx) = (1/x) + [x/(x² + 7)]
(dy/dx) = y {(1/x) + [x/(x² + 7)]}
(dy/dx) = [x √(x² + 7)] {(1/x) + [x/(x² + 7)]}
2018-04-08 10:32 pm
Both factors are positive so we can apply the log to both membres
log y=log (x*√(x²+7))
logy=logx+(1/2)log(x²+7)
derivative. Note the first member is a compound function so we have to apply the chain rule. dlogy/dy*dy/dx
(1/y)*dy/dx=1/x+(1/2)(1/(x²+7) *2x)
dy/dx=y*(1/x+x/(x²+7))
dy/dx=(x*√(x²+7))*(1/x+x/(x²+7))
dy/dx=(2x²+7)/√(x²+7) with x>0
log y=log (x*√(x²+7))
logy=logx+(1/2)log(x²+7)
derivative. Note the first member is a compound function so we have to apply the chain rule. dlogy/dy*dy/dx
(1/y)*dy/dx=1/x+(1/2)(1/(x²+7) *2x)
dy/dx=y*(1/x+x/(x²+7))
dy/dx=(x*√(x²+7))*(1/x+x/(x²+7))
dy/dx=(2x²+7)/√(x²+7) with x>0
2018-04-09 2:29 am
lny = lnx + 1/2 ln(x² + 7)
y/y’ = x + 1/2 (x² + 7)/(2x)
Solve algebraically for y’
y/y’ = x + 1/2 (x² + 7)/(2x)
Solve algebraically for y’
2018-04-09 12:29 am
y = x(x^2 + 7)^(1/2)
Use Product Rule
dy/dx = vdu + u dv
Hence
dy/dx = x(1/2)(x^2 + 7)^(-1/2)(2x) + (1)(x^2 + 7)^(1/2)
Tidying up
dy/dx = 2x^2 / [(2(x^2 + 7)^(1/2)] + (x^2 + 7)^(1/2)
or
dy/dx = 2x^2 + 2(x^2 + 7) / (2(x^2 + 7)^(1/2)
dy/dx = (4x^2 + 14) / ( 2(x^2 + 7)^(1/2))
dy/dx = (2x^2 + 7) / (x^2 + 7)^(1/2)
Use Product Rule
dy/dx = vdu + u dv
Hence
dy/dx = x(1/2)(x^2 + 7)^(-1/2)(2x) + (1)(x^2 + 7)^(1/2)
Tidying up
dy/dx = 2x^2 / [(2(x^2 + 7)^(1/2)] + (x^2 + 7)^(1/2)
or
dy/dx = 2x^2 + 2(x^2 + 7) / (2(x^2 + 7)^(1/2)
dy/dx = (4x^2 + 14) / ( 2(x^2 + 7)^(1/2))
dy/dx = (2x^2 + 7) / (x^2 + 7)^(1/2)
2018-04-08 10:41 pm
ln(y) = ln(x) + (1/2)ln(x^2 + 7) =>
(1/y) dy/dx = 1/x + x/(x^2 + 7) =>
dy/dx = y/x + xy/(x^2 + 7) .
If you want to replace the "y" with its equivalent and complete the algebra, I leave that to you.
(1/y) dy/dx = 1/x + x/(x^2 + 7) =>
dy/dx = y/x + xy/(x^2 + 7) .
If you want to replace the "y" with its equivalent and complete the algebra, I leave that to you.
收錄日期: 2021-04-24 01:01:20
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20180408140958AAvygkN

