Find all possible coordinates for S?

For parallelogram PQRS :

Mid-point of QS = Mid-point of PR
(5 + x)/2 = (-1 + 2)/2 and (5 + y)/2 = (2 - 1)/2
5 + x = 1 and 5 + y = 1
x = -4 and y = -4

S(x, y) = S(4, 4)


For parallelogram PQSR :

Mid-point of PS = Mid-point of QR
(-1 + x)/2 = (5 + 2)/2 and (2 + y)/2 = (5 - 1)/2
-1 + x = 7 and 2 + y = 4
x = 8 and y = 2

S(x, y) = S(8, 2)


For parallelogram PRQS :

Mid-point of RS = Mid-point of PQ
(2 + x)/2 = (-1 + 5)/2 and (-1 + y)/2 = (2 + 5)/2
2 + x = 4 and -1 + y = 7
x = 2 and y = 8

S(x, y) = S(2, 8)


Hence, S(x, y) = S(4,4), S(8,2) or S(2,8)

S could be diagonally opposite:
1) P, at Q+R-P, which is (5, 5) + (2, -1) - (-1, 2) which simplifies to (8, 2)
2) Q, at P+R-Q, which is ...
3) R, at P+Q-R, which is ...

This is because the intersection of the diagonals of a parallelogram is their midpoint, so in the first case (P+S)/2 = (Q+R)/2, and this becomes S = Q+R-P. I leave the second and third cases for you to solve.

P (- 1 ; 2) Q (5 ; 5) R (2 ; - 1) S (x ; y)

A quadrilateral is a parallelogram if the diagonals bisect each other.


First case, the diagonals are [QR] and [PS]

Middle of the diagonal [QR] → the point M

xM = (xQ + xR)/2 = (5 + 2)/2 = 7/2

yM = (yQ + yR)/2 = (5 - 1)/2 = 2

→ M (7/2 ; 2)

Middle of [PS] → the point M

xM = (xP + x)/2 = 7/2 → xP + x = 7 → x = 7 - xP → x = 7 + 1 → x = 8

yM = (yP + y)/2 = 2 → yP + y = 4 → y = 4 - yP → y = 4 - 2 → y = 2

→ S (8 ; 2)


Second case, the diagonals are [PR] and [QS]

Middle of the diagonal [PQ] → the point N

xM = (xP + xR)/2 = (- 1 + 2)/2 = 1/2

yM = (yP + yR)/2 = (2 - 1)/2 = 1/2

→ N (1/2 ; 1/2)

Middle of [QS] → the point N

xM = (xQ + x)/2 = 1/2 → xQ + x = 1 → x = 1 - xQ → x = 1 - 5 → x = - 4

yM = (yQ + y)/2 = 1/2 → yQ + y = 1 → y = 1 - yQ → y = 1 - 5 → y = - 4

→ S (- 4 ; - 4)

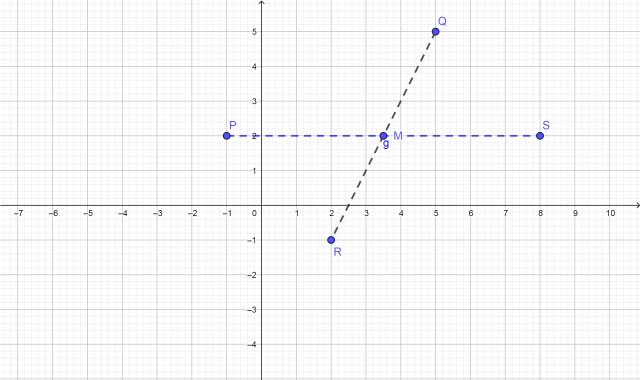
1. Figure out the midpoint M of QR
Mx=(Qx+Rx)/2=7/2
My=(Qy+Ry)/2=2
M(7/2,2)
2. Being the midpoint of QR the same of PS, we can determinate S coordinates.
From
2.1
Mx=(Px+Sx)/2 ⇒
Sx=2*Mx-Px=2*7/2-(-1)=8
2.2
My=(Py+Sy)/2 ⇒
Sy=2*My-Py=2*2-2=2

S(8,2)