(1 point) The velocity of a particle moving along a line is given by v(t)=t^3−3t^2 meters per second. Find the displacement of the particle during the time interval between -2 and 4 seconds.
I found that displacement = -12m, by taking the antiderivative and then integrating from -2 to 4
Here's the part I don't understand (see picture)
I have no idea where to go from here, if could someone please direct me?
Finding total distance with integration?
2018-02-06 2:09 pm

回答 (5)
2018-02-06 2:53 pm
t³ - 3t² = t²(t - 3)
When -2 ≤ t < 3, t³ - 3t² = t²(t - 3) < 0 and thus |t³ - 3t²| = -(t³ - 3t²)
When 3 ≤ t ≤ 4, t³ - 3t² = t²(t - 3) ≥ 0 and thus |t³ - 3t²| = t³ - 3t²
Hence,
v₁(t) = -(t³ - 3t²)
v₂(t) = t³ - 3t²
k = 3
When -2 ≤ t < 3, t³ - 3t² = t²(t - 3) < 0 and thus |t³ - 3t²| = -(t³ - 3t²)
When 3 ≤ t ≤ 4, t³ - 3t² = t²(t - 3) ≥ 0 and thus |t³ - 3t²| = t³ - 3t²
Hence,
v₁(t) = -(t³ - 3t²)
v₂(t) = t³ - 3t²
k = 3
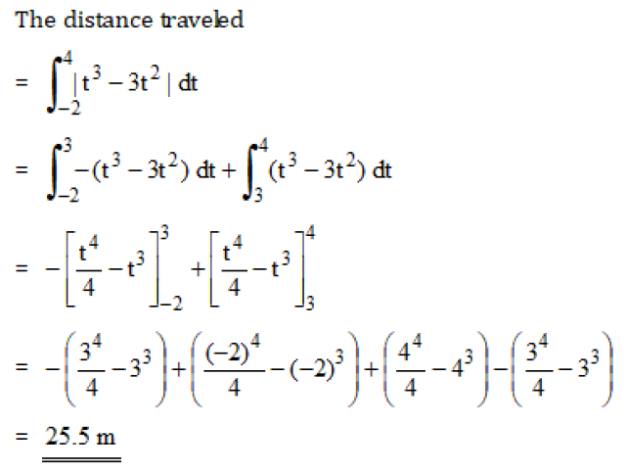
2018-02-06 3:00 pm
The difference is in the definition of "displacement" and "distance traveled". The displacement is simply the difference in position between the start of the time interval and the end of the time interval. Distance traveled is not a signed number. An example might show the difference. Assume that the particle from time t₀ to t₁ moves 5 units to the left and then 5 units to the right so that its position at t₁ is exactly the same place it was at t₀. Its displacement is zero because it's final position is the same place as it's starting position. However, the particle traveled 5 units to the left and then turned around and traveled 5 units to the right for a total distance traveled of 10 units.
When you integrate v(t)dt = (t^3−3t^2)dt from t = -2 to 4, you obtain the displacement because the distance traveled in one direction is subtracted from the distance traveled in the opposite direction. Recall that integration is actually the summing of an infinite number of signed infinitesimal steps. To find the total distance, you have to sum the absolute value of those steps so that the negative distances do not negate the positive distances.
v(t) = (t^3 - 3t^2) = t^2(t - 3)
Since t^2 is always positive for real values of t, v(t) < 0 for t < 3 and v(t) > 0 for t > 3. Therefore to get the total distance traveled we have to integrate -v(t)dt where v(t) < 0 and v(t)dt where v(t) > 0. The total distance traveled, D, becomes:
D₁ = ∫(3t² - t³)dt (integration from -2 to 3) = t³ - t⁴/4 = 3³ - 3⁴/4 - [(-2)³ - (-2)⁴/4] = 27 - 81/4 - (-8 - 4) = 75/4
D₂ = ∫(t³ - 3t²)dt (integration from 3 to 4) = t⁴/4 - t³ = 4⁴/4 - 4³ - (3⁴/4 - 3³) = 256/4 - 64 - (81/4 - 27) = 27/4
D = D₁ + D₂ = (75+27)/4 = 102/4
The answers, in terms of the problem statement are:
v₁(t) = 3t² - t³
v₂(t) = t³ - 3t²
k = 3
Total distance traveled = 102/4 or 25.5 meters
When you integrate v(t)dt = (t^3−3t^2)dt from t = -2 to 4, you obtain the displacement because the distance traveled in one direction is subtracted from the distance traveled in the opposite direction. Recall that integration is actually the summing of an infinite number of signed infinitesimal steps. To find the total distance, you have to sum the absolute value of those steps so that the negative distances do not negate the positive distances.
v(t) = (t^3 - 3t^2) = t^2(t - 3)
Since t^2 is always positive for real values of t, v(t) < 0 for t < 3 and v(t) > 0 for t > 3. Therefore to get the total distance traveled we have to integrate -v(t)dt where v(t) < 0 and v(t)dt where v(t) > 0. The total distance traveled, D, becomes:
D₁ = ∫(3t² - t³)dt (integration from -2 to 3) = t³ - t⁴/4 = 3³ - 3⁴/4 - [(-2)³ - (-2)⁴/4] = 27 - 81/4 - (-8 - 4) = 75/4
D₂ = ∫(t³ - 3t²)dt (integration from 3 to 4) = t⁴/4 - t³ = 4⁴/4 - 4³ - (3⁴/4 - 3³) = 256/4 - 64 - (81/4 - 27) = 27/4
D = D₁ + D₂ = (75+27)/4 = 102/4
The answers, in terms of the problem statement are:
v₁(t) = 3t² - t³
v₂(t) = t³ - 3t²
k = 3
Total distance traveled = 102/4 or 25.5 meters
2018-02-06 2:45 pm
∫ |t^3−3t^2| dt [-2, 4] = ∫ -(t^3−3t^2) dt [-2, 3] + ∫ (t^3−3t^2) dt [3, 4] = 25.5
v₁(t) = (3t^2 - t^3)
v₂(t) = (t^3 - 3t^2)
k = 3
Total distance travelled = 25.5 m
here is a graph for you:
https://www.desmos.com/calculator/1ahsp5dtyd
I hope this helps.
v₁(t) = (3t^2 - t^3)
v₂(t) = (t^3 - 3t^2)
k = 3
Total distance travelled = 25.5 m
here is a graph for you:
https://www.desmos.com/calculator/1ahsp5dtyd
I hope this helps.
2018-02-06 9:36 pm
Here's the graph of v(t)
http://www.wolframalpha.com/input/?i=graph+x%5E3-3x%5E2+from+-2+to+4
from -2 to 3, v(t) < 0
|t^3-3t^2| = 3t^2-t^3
from 3 to 4 , v(t) > 0
|t^3-3t^2| = t^3-3t^2
The first integral is ∫ [-2,3] (3t^2-t^3) dt
The second integral is ∫ [3, 4] (t^3-3t^2) dt
∫ (3t^2-t^3) = 3(t^3/3)-t^4/ 4 = t^3 -(1/4)t^4
F(t) = t^3 -(1/4)t^4
F(3) = 3^3 - (1/4) 3^4 = 27/4
F(-2) = (-2)^3 -(1/4) (-2)^4 = -8 - 16/4 = -12
F(3)-F(-2) = 27/4-(-12) = 75/4
First integral is 75/4
∫ (t^3-3t^2) = (1/4)t^4 - t^3
F(t) = (1/4)t^4 -t^3
F(4) = 4^4 /4 - 4^3 = 64-64=0
F(3) = 3^4 /4 - 3^3 = -27/4
F(4)-F(3) = 0-(-27/4)= 27/4
Second integral is 27/4
(1)+(2) = 75/4+27/4 = 51/2 = 25.5
http://www.wolframalpha.com/input/?i=graph+x%5E3-3x%5E2+from+-2+to+4
from -2 to 3, v(t) < 0
|t^3-3t^2| = 3t^2-t^3
from 3 to 4 , v(t) > 0
|t^3-3t^2| = t^3-3t^2
The first integral is ∫ [-2,3] (3t^2-t^3) dt
The second integral is ∫ [3, 4] (t^3-3t^2) dt
∫ (3t^2-t^3) = 3(t^3/3)-t^4/ 4 = t^3 -(1/4)t^4
F(t) = t^3 -(1/4)t^4
F(3) = 3^3 - (1/4) 3^4 = 27/4
F(-2) = (-2)^3 -(1/4) (-2)^4 = -8 - 16/4 = -12
F(3)-F(-2) = 27/4-(-12) = 75/4
First integral is 75/4
∫ (t^3-3t^2) = (1/4)t^4 - t^3
F(t) = (1/4)t^4 -t^3
F(4) = 4^4 /4 - 4^3 = 64-64=0
F(3) = 3^4 /4 - 3^3 = -27/4
F(4)-F(3) = 0-(-27/4)= 27/4
Second integral is 27/4
(1)+(2) = 75/4+27/4 = 51/2 = 25.5
2018-02-06 2:40 pm
The function changes sign between the limits of integration, at k. You need to find k, then you integrate v(t) where v(t) >= 0, and -v(t) where v(t) <= 0.
It has another 0 in that range, but it's a double zero so the graph doesn't cross the x-axis.
You get rid of the absolute value symbols by just using an expression which you know is > 0 and equal to the absolute value.
It has another 0 in that range, but it's a double zero so the graph doesn't cross the x-axis.
You get rid of the absolute value symbols by just using an expression which you know is > 0 and equal to the absolute value.
收錄日期: 2021-04-18 18:05:19
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20180206060906AA27JNA

