I need help with this question please!?
2018-01-03 3:15 am
Find the equation of the line tangent to the parabola y equals x squared minus 3 x plus 2 and perpendicular to the line 5 x minus 2 y minus 10 equals 0.
回答 (3)
2018-01-03 5:43 am
5x-2y-10 = 0
y = (5/2)x - 5
slope of line is (5/2)
slope of perpendicular to the line is -⅖ = -0.4
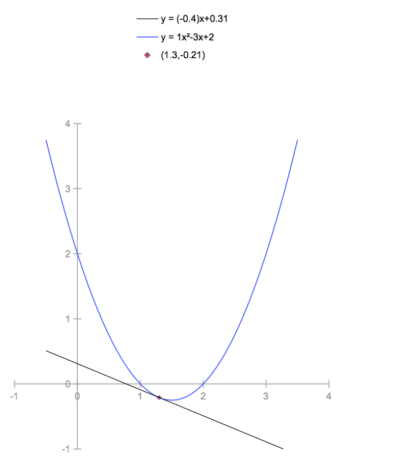
y = x²-3x+2
slope of tangent = dy/dx = 2x-3
2x-3 = -0.4
x = 1.3
y = -0.21
Slope of tangent line at (1.3,-0.21) is -0.4
tangent line:
y+0.21 = -0.4(x-1.3)
y = -0.4x + 0.31
y = (5/2)x - 5
slope of line is (5/2)
slope of perpendicular to the line is -⅖ = -0.4
y = x²-3x+2
slope of tangent = dy/dx = 2x-3
2x-3 = -0.4
x = 1.3
y = -0.21
Slope of tangent line at (1.3,-0.21) is -0.4
tangent line:
y+0.21 = -0.4(x-1.3)
y = -0.4x + 0.31
2018-01-03 3:49 am
Parabola: P: y = x^2 - 3x + 2
Rerefence line: R: 5x - 2y - 10 = 0
The requested line L will have an equation of L: y = mx + b
Where m is its slope and b its "elevation" over (or under) point O(0,0)
Now, since L and R are perpendicular to each other, the product of their slopes must equal -1
Slope of R: 5x - 2y - 10 = 0 <=> 2y = 5x - 10 <=> y = 5/2 x - 5, therefore its slope is 5/2
It must therefore be that m * 5/2 = -1 <=> m = -2/5
Therefore L becomes: L: y = (-2/5)x + b
Since L is tangent to P, their system of simultaneous equations must yield a SINGLE solution (if L and P didn't intersect at all it would have to yield no solutions, and if they weren't tangential but properly intersected then it would have to yield two distinct solutions).
Therefore, if we substitute y from L into P:
P: y = x^2 - 3x + 2 ==> (-2/5)x + b = x^2 - 3x + 2 <=> x^2 + (2/5 - 3)x + (2-b) = 0 <=> x^2 - (13/5) x + (2-b) = 0
The above resulting quadratic equation must yield a SINGLE solution. This can only happen if its discriminant is 0, therefore it must hold that:
(13/5)^2 - 4 * (2-b) = 0 <=> (13/5)^2 - 8 + 4b = 0 <=> 4b = 8 - 169/25 = 31/25 <=> b = 31/100
So: m = -2/5 , b = 31/100 and line L is: y = (-2/5)x + 31/200 or y = -0.4x + 0.31
Rerefence line: R: 5x - 2y - 10 = 0
The requested line L will have an equation of L: y = mx + b
Where m is its slope and b its "elevation" over (or under) point O(0,0)
Now, since L and R are perpendicular to each other, the product of their slopes must equal -1
Slope of R: 5x - 2y - 10 = 0 <=> 2y = 5x - 10 <=> y = 5/2 x - 5, therefore its slope is 5/2
It must therefore be that m * 5/2 = -1 <=> m = -2/5
Therefore L becomes: L: y = (-2/5)x + b
Since L is tangent to P, their system of simultaneous equations must yield a SINGLE solution (if L and P didn't intersect at all it would have to yield no solutions, and if they weren't tangential but properly intersected then it would have to yield two distinct solutions).
Therefore, if we substitute y from L into P:
P: y = x^2 - 3x + 2 ==> (-2/5)x + b = x^2 - 3x + 2 <=> x^2 + (2/5 - 3)x + (2-b) = 0 <=> x^2 - (13/5) x + (2-b) = 0
The above resulting quadratic equation must yield a SINGLE solution. This can only happen if its discriminant is 0, therefore it must hold that:
(13/5)^2 - 4 * (2-b) = 0 <=> (13/5)^2 - 8 + 4b = 0 <=> 4b = 8 - 169/25 = 31/25 <=> b = 31/100
So: m = -2/5 , b = 31/100 and line L is: y = (-2/5)x + 31/200 or y = -0.4x + 0.31
2018-01-03 3:49 am
You sure do need help, Mr. minus plus plus plus minus minus plus minus minus plus.
The question has a parabola. y = x^2 - 3x + 2
We are to find the tangent line to that parabola.
Any a specific tangent line: it needs to be perpendicular to line 5x - 2y - 10 = 0
5x - 2y - 10 = 0 ===> y = (5/2)x + 5
Given line has slope 5/2.
Perpendicular lines' slopes have to multiply together to give -1: so tangent line has slope -2/5.
Which tangent line to parabola has slope -2/5? Differentiate parabola.
y' = 2x - 3
This is the slope of the tangent depending on the x-coordinate of the point it's tangent to. We want it to be -2/5, so what's that x-coordinate?
2x - 3 = -2/5
x = 13/10
What's the y-coordinate? Plug into parabola.
y = x^2 - 3x + 2 = -0.21
With point (1.3, -0.21) and slope -2/5, the line is
y + 0.21 = (-2/5)(x - 1.3)
Very simple.
The question has a parabola. y = x^2 - 3x + 2
We are to find the tangent line to that parabola.
Any a specific tangent line: it needs to be perpendicular to line 5x - 2y - 10 = 0
5x - 2y - 10 = 0 ===> y = (5/2)x + 5
Given line has slope 5/2.
Perpendicular lines' slopes have to multiply together to give -1: so tangent line has slope -2/5.
Which tangent line to parabola has slope -2/5? Differentiate parabola.
y' = 2x - 3
This is the slope of the tangent depending on the x-coordinate of the point it's tangent to. We want it to be -2/5, so what's that x-coordinate?
2x - 3 = -2/5
x = 13/10
What's the y-coordinate? Plug into parabola.
y = x^2 - 3x + 2 = -0.21
With point (1.3, -0.21) and slope -2/5, the line is
y + 0.21 = (-2/5)(x - 1.3)
Very simple.
收錄日期: 2021-05-01 22:14:12
原文連結 [永久失效]:
https://hk.answers.yahoo.com/question/index?qid=20180102191542AAliCVZ

