maths help!!!!!!!!!!?

7.

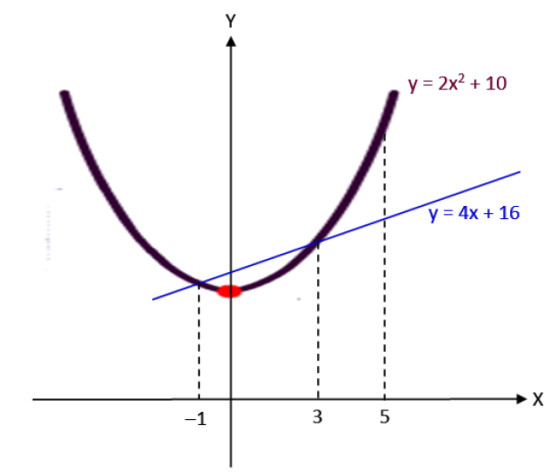
Find the points of intersection of y = 2x² + 10 and y = 4x + 16 :
2x² + 10 = 4x + 16
x² + 5 = 2x + 8
x² - 2x - 3 = 0
(x + 1)(x - 3) = 0
x = -1 or x = 3
Then, the two curves meet at x = -1 and x = 3

The two curves are shown in the diagram below. (The diagram is not to scale.)


Area of the region bounded by (y = 2x² + 10, y = 4x + 16, x = -1 and x = 5)
= ∫₋₁³ [(4x + 16) - (2x² + 10)] dx + ∫₃⁵ [(2x² + 10) - (4x + 16)] dx
= ∫₋₁³ (-2x² + 4x + 6) dx + ∫₃⁵ (2x² - 4x - 6) dx
= [-(2/3)x³ + 2x² + 6x]₋₁³ + [(2/3)x³ - 2x² - 6x]₃⁵
= [-(2/3)(3)³ + 2(3)² + 6(3)] - [-(2/3)(-1)³ + 2(-1)² + 6(-1)] + [(2/3)(5)³ - 2(5)² - 6(5)] - [(2/3)(3)³ - 2(3)² - 6(3)]
= 18 - (-10/3) + (10/3) - (-18)
= 128/3 (sq. units)

y=2x^2+10
y= 4x+16

2x^2+10 = 4x+16
2x^2-4x-6 = 0
x^2-2x-3=0
(x-3)(x+1)=0
x=-1 ; x=3 are points of intersection of the two curves.

http://www.wolframalpha.com/input/?i=graph+2x%5E2%2B10+and+4x%2B16+from+-1+to+5
Integrate from -1 to 3 and then from 3 to 5

Area = & (4x+16-2x^2-10) dx
= & (4x-2x^2+6) dx
= 4& x -2 & x^2 + 6& dx
= (4/2) x^2 -(2/3)x^3 + 6x
= 2x^2-(2/3)x^3 + 6x
From -1 to 3, 4x+16 > 2x^2+10

F(x) = 2x^2 -(2/3) x^3 + 6x
F(3) = 18
F(-1) = -10/3
F(3)-F(-1) = 18+10/3 = 64/3 ---------(1)

From 1 to 5, 2x^2+10 > 4x+16

Area = & (2x^2+10-4x-16) dx
= & (2x^2-4x-6) dx
= (2/3) x^3 - 2x^2 - 6x

F(x) = (2/3)x^3 - 2x^2-6x
F(5) = 10/3
F(3) = -18
F(5)-F(3) = 10/3 -(-18) = 10/3 +18 = 64/3 ------(2)

Area = (1)+(2) = 128/3

2x^2 + 10 = 4x + 16
2x^2 - 4x - 6 = 0
x^2 - 2x - 3 = 0
(x - 3)(x + 1) = 0
x = 3 and x = -1
4x + 16 > 2x^2 + 10 for x in [-1, 3).
2x^2 + 10 > 4x + 16 for x in (3, 5].
Therefore, area =
3
∫ 4x + 16 - (2x^2 + 10) dx +
-1

5
∫ 2x^2 + 10 - (4x + 16) dx =
3

3
∫ -2x^2 + 4x + 6 dx +
-1

5
∫ 2x^2 - 4x - 6 dx =
3
................................3
-2x^3/3 + 2x^2 + 6x | +
..............................-1

.............................5
2x^3/3 - 2x^2 - 6x | =
............................3

-18 + 18 + 18 - (2/3 + 2 - 6) + 250/3 - 50 - 30 - (18 - 18 - 18) =
18 - 2/3 + 4 + 250/3 - 80 + 18 =
-40 + 248/3 =
-120/3 + 248/3 =
128/3